La régression est utilisée pour modéliser la relation entre une variable de réponse et une ou plusieurs variables prédictives. STATGRAPHICS Centurion fournit un grand nombre de procédures pour ajuster différents types de modèles de régression.
Méthodes de régression
Régression simple
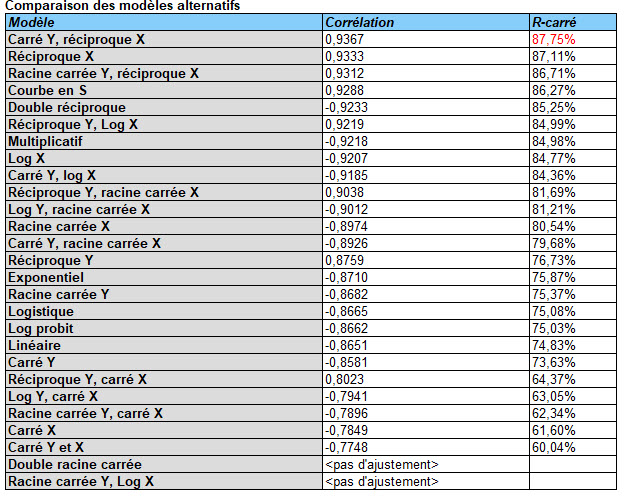
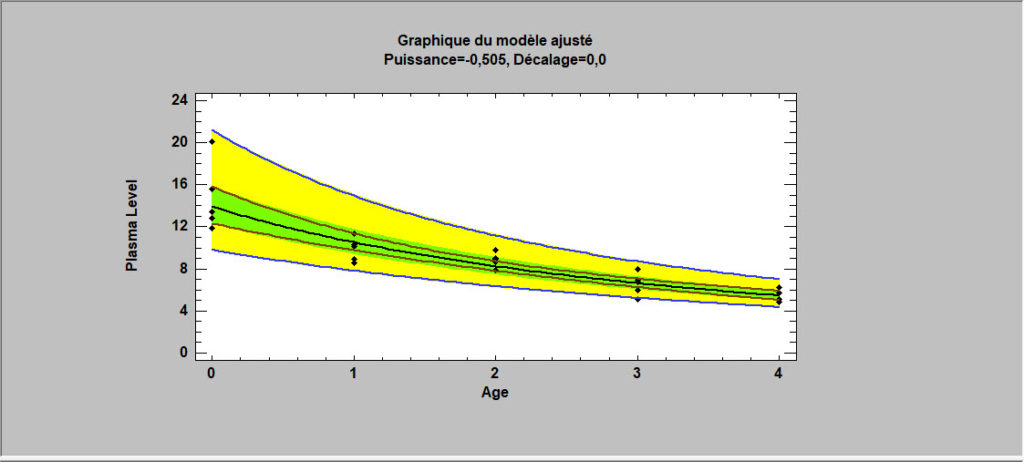
Les modèles de régression les plus simples impliquent une seule variable de réponse Y et une seule variable prédictive X. STATGRAPHICS permet de choisir une variété de formes fonctionnelles et classe les modèles par ordre décroissant de R-carré. Si des valeurs aberrantes sont suspectées, des méthodes robustes peuvent être utilisées pour ajuster les modèles en remplacement de la méthode des moindres carrés.
Transformations Box-Cox
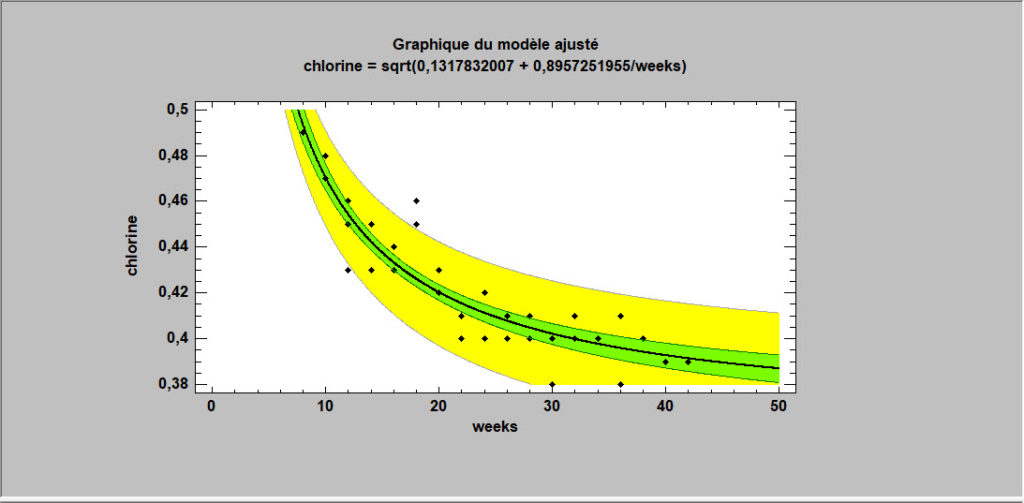
Lorsque la variable de réponse ne suit pas une loi normale, il est parfois possible d’utiliser les méthodes de Box et Cox pour trouver une transformation qui améliore l’ajustement. Leurs transformations sont basées sur les puissances de Y. STATGRAPHICS déterminera automatiquement la puissance optimale et adaptera un modèle approprié.
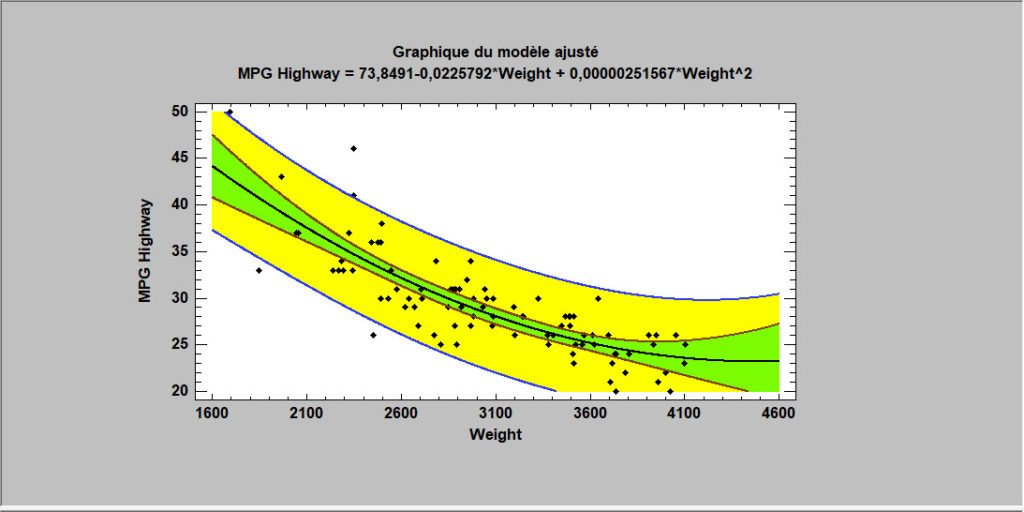
Régression polynomiale
Une autre approche pour ajuster une équation non linéaire consiste à considérer les fonctions polynomiales de X. À des fins d’interpolation, les polynômes ont la propriété intéressante de pouvoir approximer de nombreux types de fonctions.
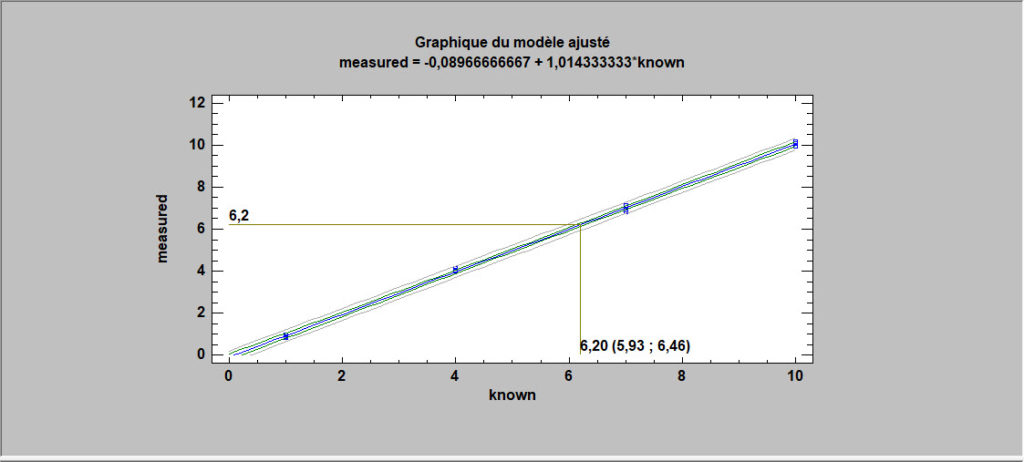
Modèles d’étalonnage
Dans un problème d’étalonnage typique, un certain nombre d’échantillons connus sont mesurés et une équation est ajustée reliant les mesures aux valeurs de référence. L’équation ajustée est ensuite utilisée pour prévoir la valeur d’un échantillon inconnu en générant une prévision inverse (prévision de X à partir de Y) après avoir mesuré l’échantillon.
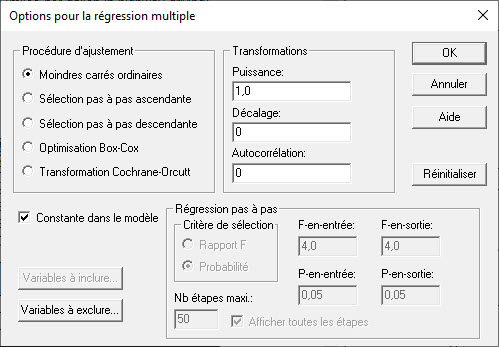
Régression multiple
La procédure de régression multiple ajuste un modèle reliant une variable de réponse Y à plusieurs variables prédictives X1, X2, … . L’utilisateur peut inclure toutes les variables prédictives dans l’ajustement ou demander au programme d’utiliser une régression pas à pas pour sélectionner un sous-ensemble contenant uniquement des prédicteurs significatifs. De plus, la méthode de Box-Cox peut être utilisée pour traiter la non-normalité et la procédure de Cochrane-Orcutt pour traiter les résidus autocorrélés.
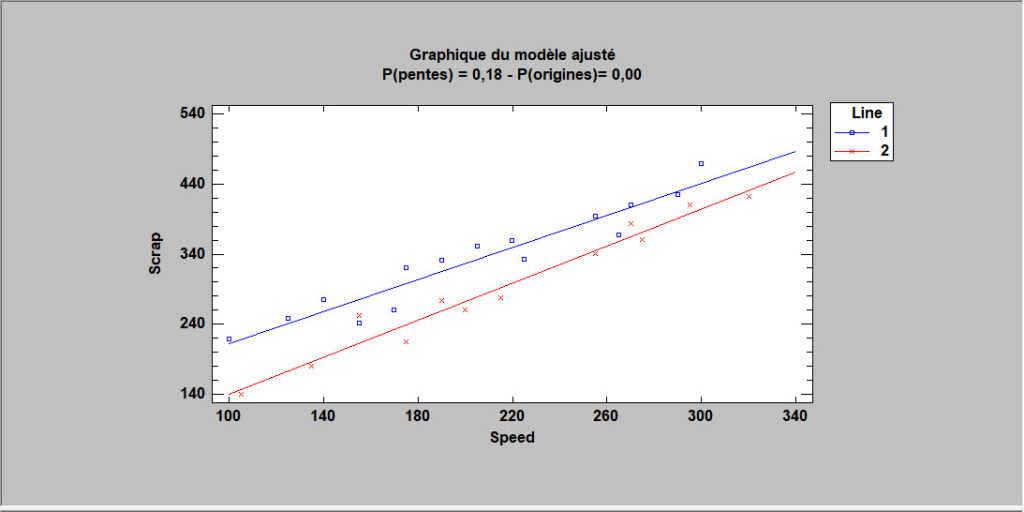
Comparaison de droites de régression
Dans certaines situations, il est nécessaire de comparer plusieurs droites de régression. STATGRAPHICS ajustera des régressions linéaires parallèles ou non parallèles pour chaque niveau d’une variable de codes et effectuera des tests statistiques pour déterminer si les valeurs à l’origine et/ou les pentes des lignes sont significativement différentes.
Sélection du meilleur modèle de régression
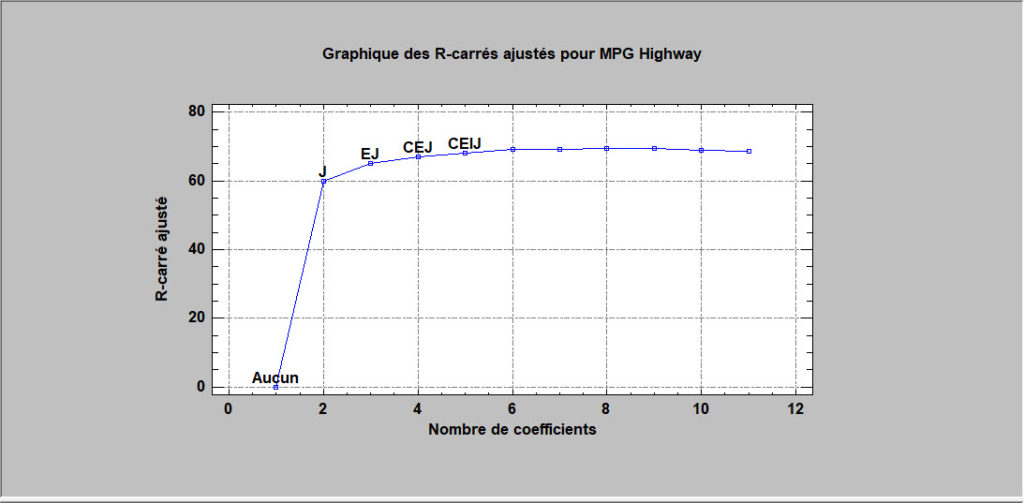
Si le nombre de prédicteurs n’est pas trop important, il est possible d’ajuster des modèles de régression impliquant toutes les combinaisons de 1 prédicteur, 2 prédicteurs, 3 prédicteurs, etc., et de trier les modèles selon une statistique de qualité d’ajustement. Dans STATGRAPHICS, la procédure permet de sélectionner les modèles qui donnent les meilleures valeurs du R-carré ajusté ou de la statistique Cp de Mallows.
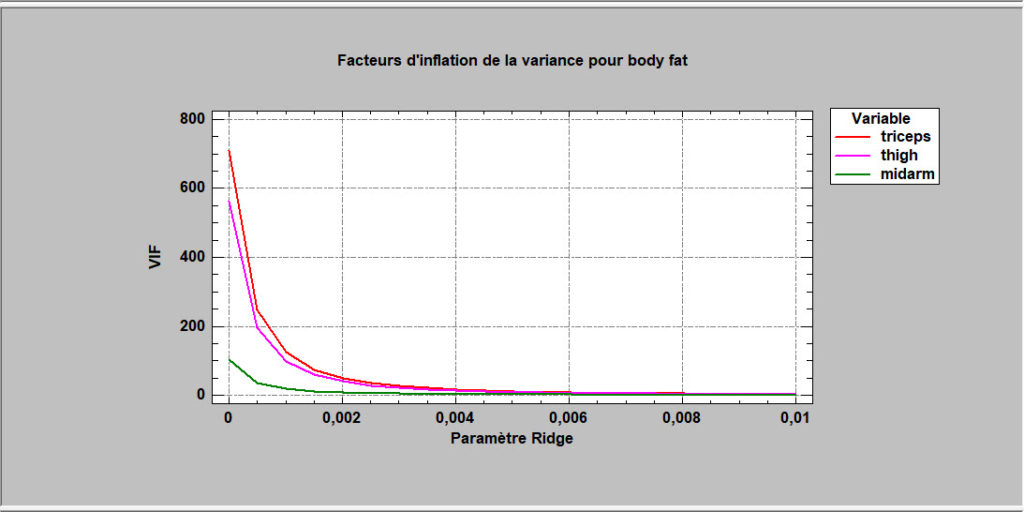
Régression Ridge
Lorsque les variables prédictives sont fortement corrélées entre elles, les coefficients de l’ajustement des moindres carrés résultant peuvent être très imprécis. En autorisant un léger biais dans les estimations, des coefficients plus raisonnables peuvent souvent être obtenus. La régression Ridge est une méthode pour résoudre ces problèmes. Souvent, de petites quantités de biais entraînent des réductions spectaculaires de la variance des coefficients estimés du modèle.
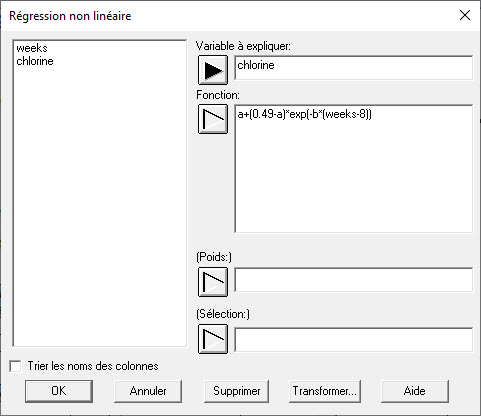
Régression non linéaire
La plupart des procédures de régression des moindres carrés sont conçus pour ajuster des modèles qui sont linéaires par rapport aux coefficients. Lorsque l’analyste souhaite ajuster un modèle intrinsèquement non linéaire, une procédure numérique doit être utilisée. La procédure des moindres carrés non linéaires de STATGRAPHICS utilise un algorithme dû à Marquardt pour ajuster toute fonction entrée par l’utilisateur.
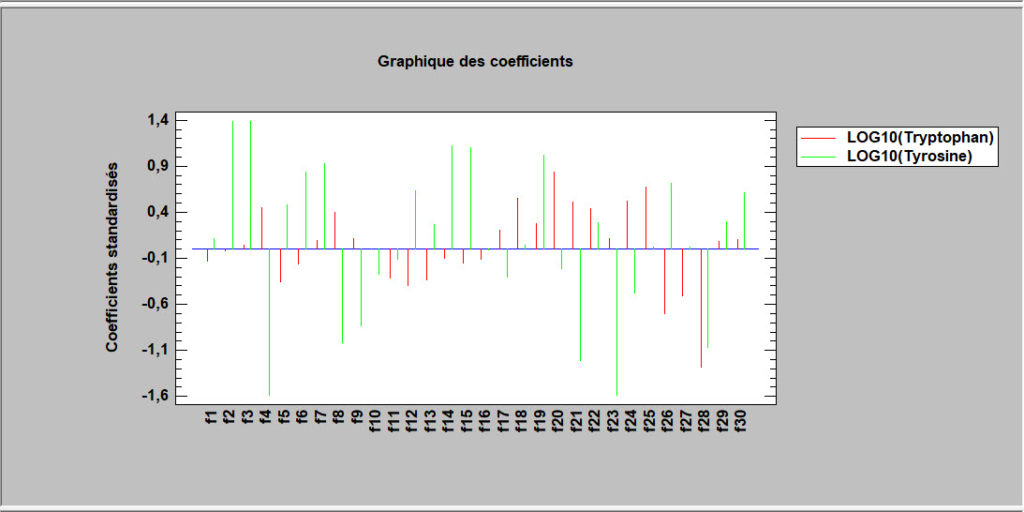
Moindres carrés partiels (PLS)
Les moindres carrés partiels sont conçus pour construire un modèle statistique reliant plusieurs variables indépendantes X à une ou plusieurs variables dépendantes Y. La procédure est particulièrement utile lorsqu’il existe de nombreux prédicteurs et que l’objectif principal de l’analyse est la prévision des variables de réponse. Contrairement à d’autres procédures de régression, des estimations peuvent être dérivées même dans le cas où le nombre de variables prédictives dépasse le nombre d’observations. La régression PLS est largement utilisée par les ingénieurs chimistes et les chimiométriciens pour l’étalonnage spectrométrique.
Modèle linéaire général (GLM)
La procédure GLM est utile lorsque les prédicteurs incluent à la fois des facteurs quantitatifs et qualitatifs. Lors de l’ajustement d’un modèle de régression, il offre la possibilité de créer facilement des tracés de surfaces et de contours.
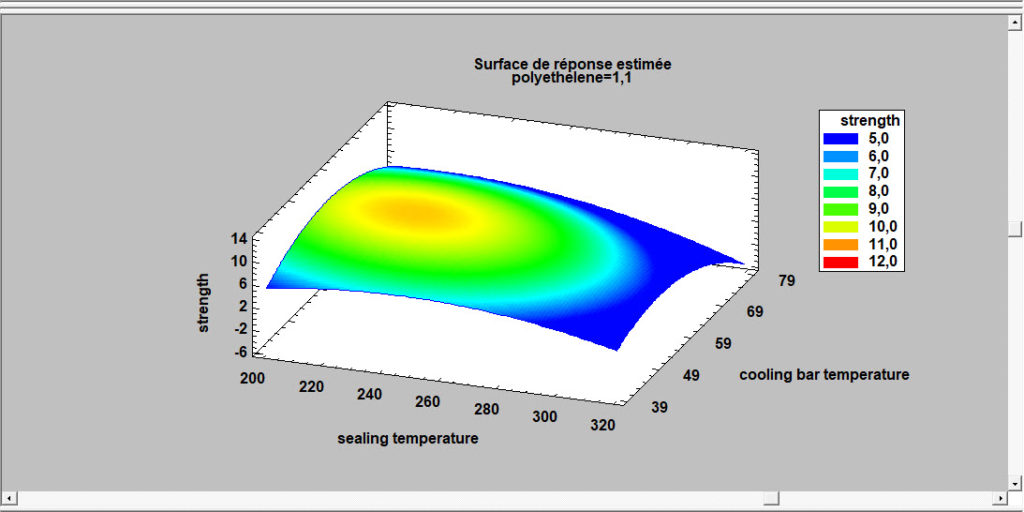
Régression sur données de survie
Pour décrire l’impact des variables externes sur les temps de défaillances, des modèles de régression peuvent être adaptés. Toutefois, les techniques standard des moindres carrés ne fonctionnent pas bien pour deux raisons : les données sont souvent censurées et la distribution des temps de défaillance est rarement gaussienne. Pour cette raison, STATGRAPHICS fournit une procédure spéciale qui ajustera les modèles de régression pour des données de survie avec censures, en supposant une distribution exponentielle, de valeur extrême, logistique, log-logistique, log-normale, normale ou de Weibull.
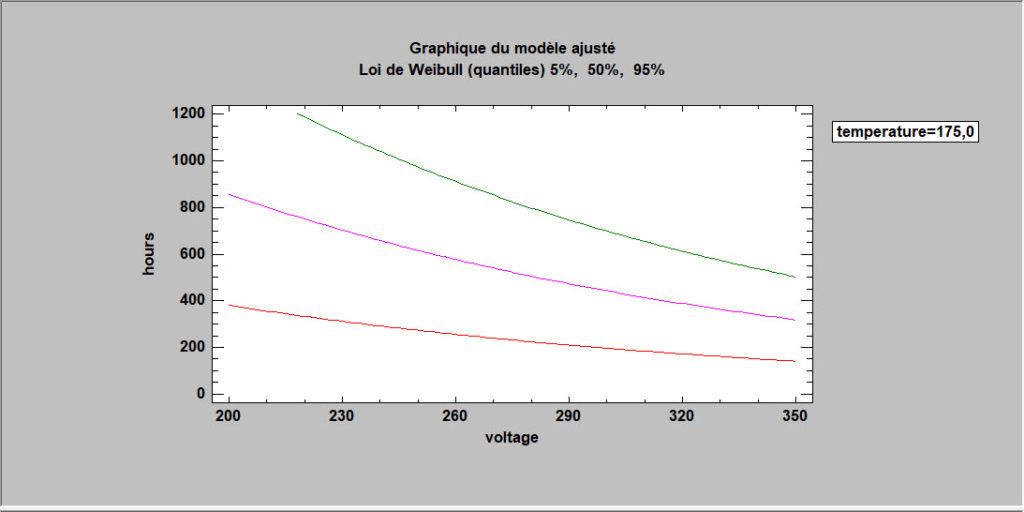
Régressions pour des proportions
Lorsque la variable de réponse est une proportion ou une valeur binaire (0 ou 1), les techniques de régression standard doivent être modifiées. STATGRAPHICS fournit deux procédures importantes pour cette situation : la régression logistique et l’analyse Probit. Les deux méthodes donnent une équation de prévision qui est contrainte de se situer entre 0 et 1.
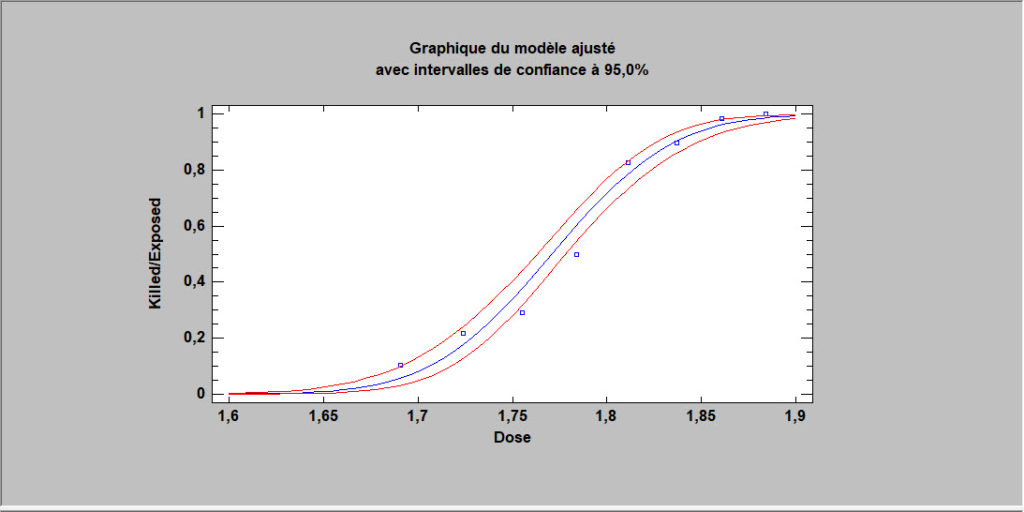
Régressions pour des comptages
Pour les variables de réponse qui sont des comptages, STATGRAPHICS fournit deux procédures : la régression de Poisson et la régression binomiale négative. Chacune ajuste un modèle log-linéaire impliquant à la fois des prédicteurs quantitatifs et qualitatifs.
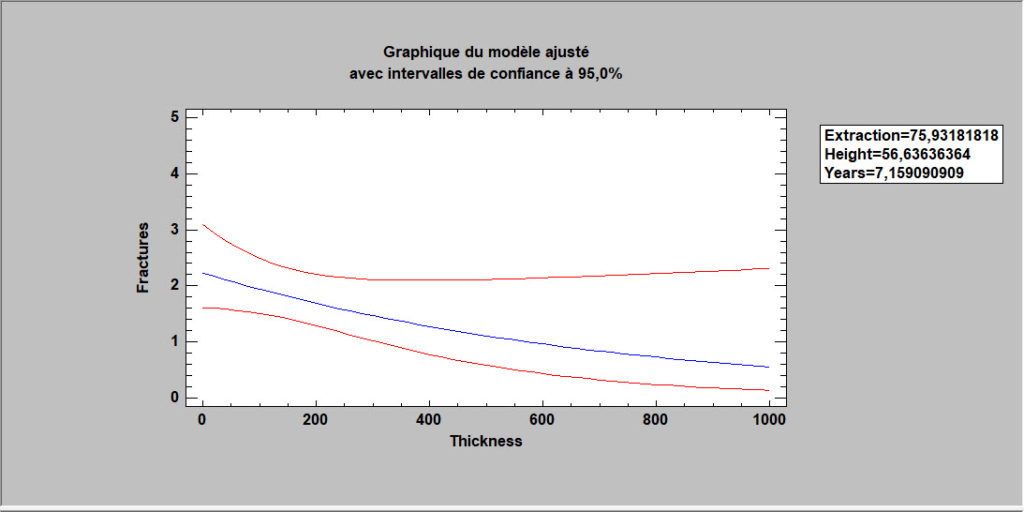
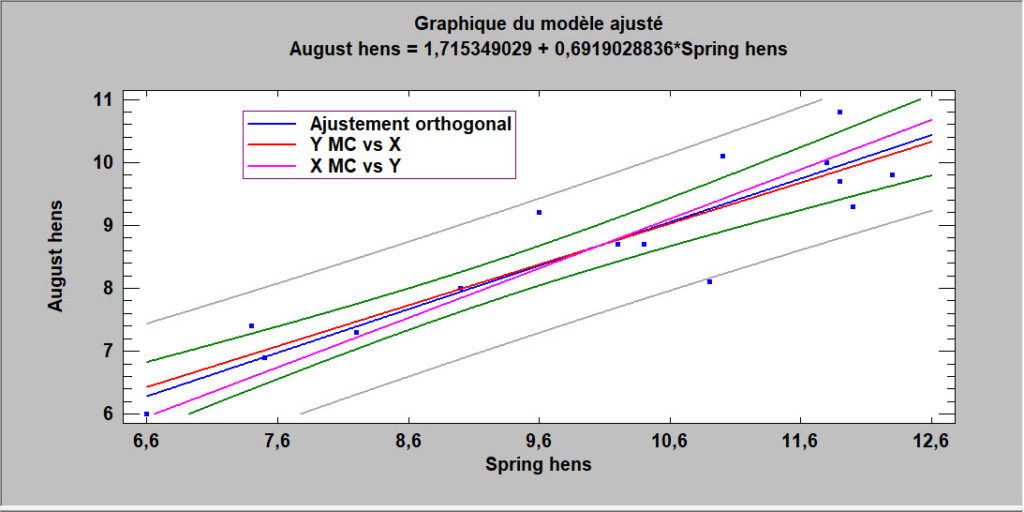
Régression orthogonale
La procédure de régression orthogonale est conçue pour construire un modèle statistique décrivant l’impact d’un seul facteur quantitatif X sur une variable dépendante Y, lorsque X et Y sont observés avec erreur. Jusqu’à 27 modèles linéaires et non linéaires peuvent être ajustés.
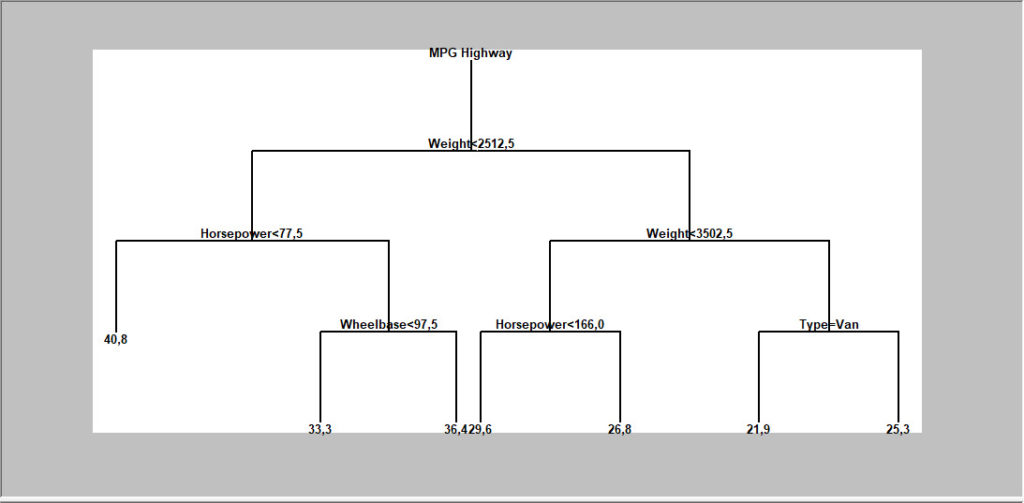
Arbres de décision et de régression
Cette procédure implémente une technique d’apprentissage machine pour prévoir des observations à partir des données. Elle crée des modèles de deux formes : arbres de décision qui découpent les observations en groupes basés sur les caractéristiques observées ou arbres de régression qui prévoient la valeur d’une variable à expliquer. Les modèles sont construits en créant un arbre dont chacun des nœuds correspond à une décision binaire. Partant d’une observation donnée, l’utilisateur parcourt les branches de l’arbre jusqu’à atteindre une feuille. Chaque feuille de l’arbre est associée à une classe ou valeur prévue.
Régression linéaire par morceaux
La procédure de régression linéaire par morceaux est conçue pour ajuster un modèle de régression où la relation entre la variable dépendante Y et la variable indépendante X est une fonction continue composée de 2 segments linéaires ou plus. La fonction est estimée à l’aide des moindres carrés non linéaires. L’utilisateur spécifie le nombre de segments et les estimations initiales des emplacements où les segments se rejoignent.
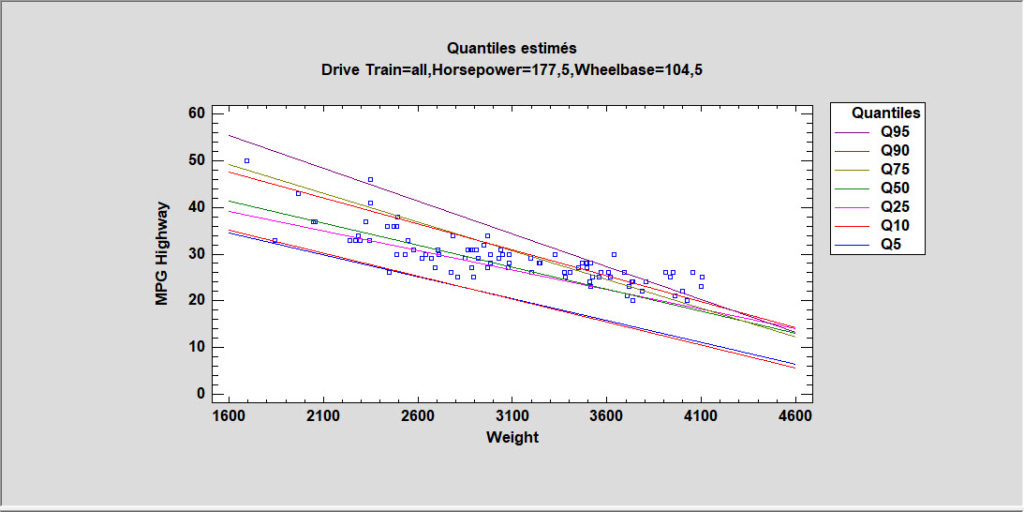
Régression quantile
La procédure de régression quantile ajuste des modèles linéaires pour décrire la relation entre les quantiles sélectionnés d’une variable dépendante Y et une ou plusieurs variables indépendantes. Les variables indépendantes peuvent être quantitatives ou qualitatives. Contrairement aux procédures de régression multiple habituel dans lesquelles le modèle est utilisé pour prédire la réponse moyenne, les modèles de régression quantile peuvent être utilisés pour prédire tout centile. La régression médiane est un cas particulier où le quantile à prédire est le 50ème centile.
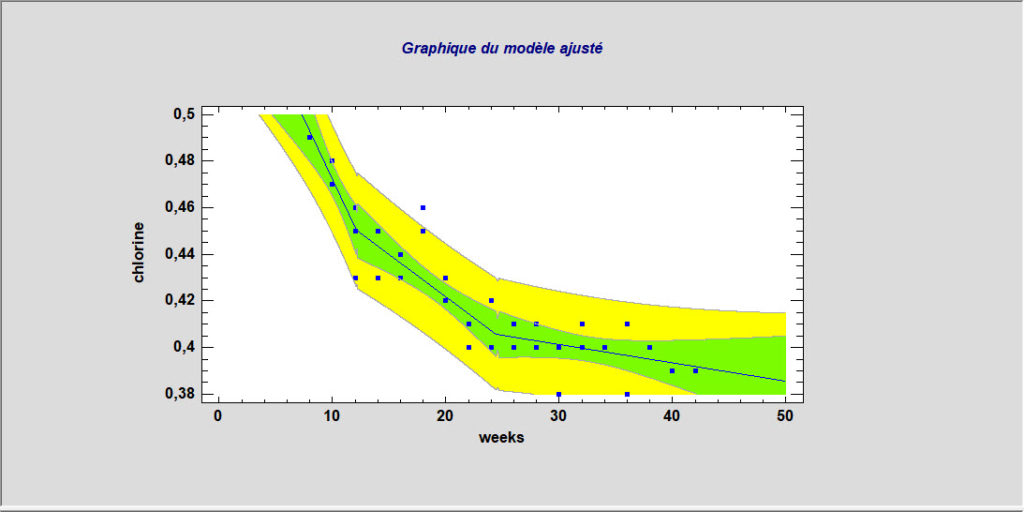
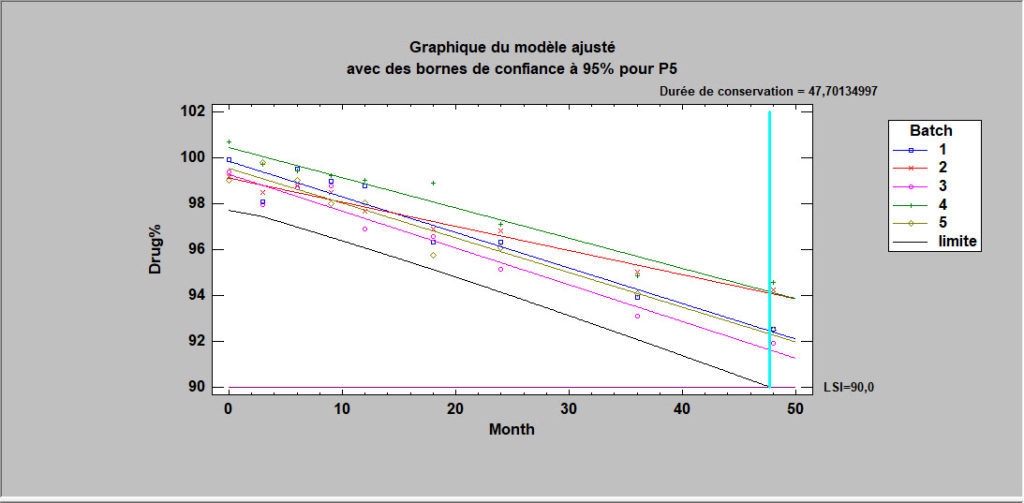
Etudes de stabilité
Les études de stabilité sont couramment utilisées par les sociétés pharmaceutiques pour estimer le taux de dégradation des médicaments et pour établir la durée de conservation. Les mesures sont généralement effectuées sur des échantillons provenant de plusieurs lots à différents moments. L’intérêt principal est d’estimer le moment auquel la limite de prévision inférieure du modèle de dégradation croise les limites des spécifications inférieures pour le médicament. Selon la structure des données, les lots peuvent être traités comme un facteur fixe ou aléatoire.
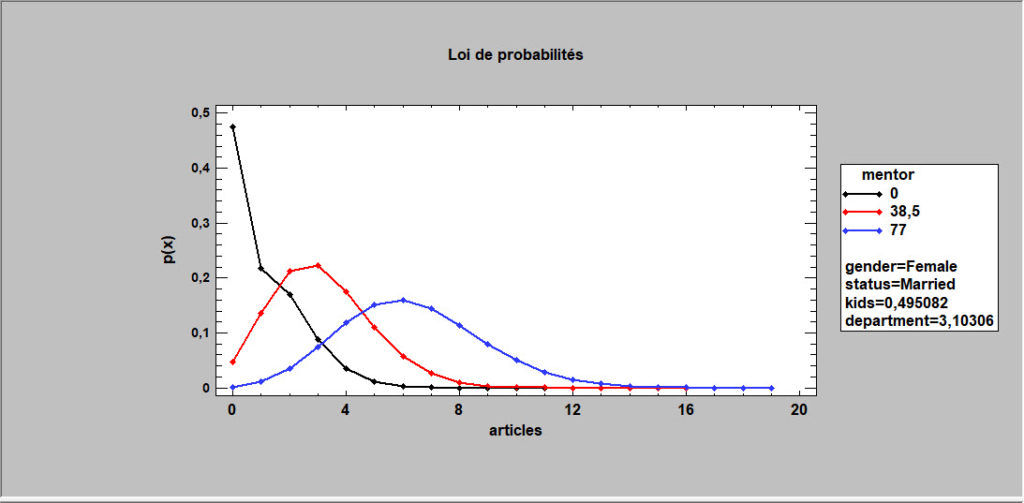
Régression à inflation de zéros
Cette procédure est conçue pour ajuster un modèle de régression dans lequel la variable dépendante Y est constituée de comptages. Le modèle de régression ajusté relie Y à une ou plusieurs variables prédictives X qui peuvent être quantitatives ou qualitatives. Il est similaire aux procédures de régression de Poisson et de régression binomiale négative, sauf qu’il contient un composant supplémentaire qui représente l’inflation de zéros. Les données contenant des zéros en excès sont très courantes comme le nombre de jours d’absence d’un élève à l’école, le nombre de réclamations concernant une assurance au sein d’une population où tout le monde n’a pas d’assurance, le nombre de défauts dans un article manufacturé.