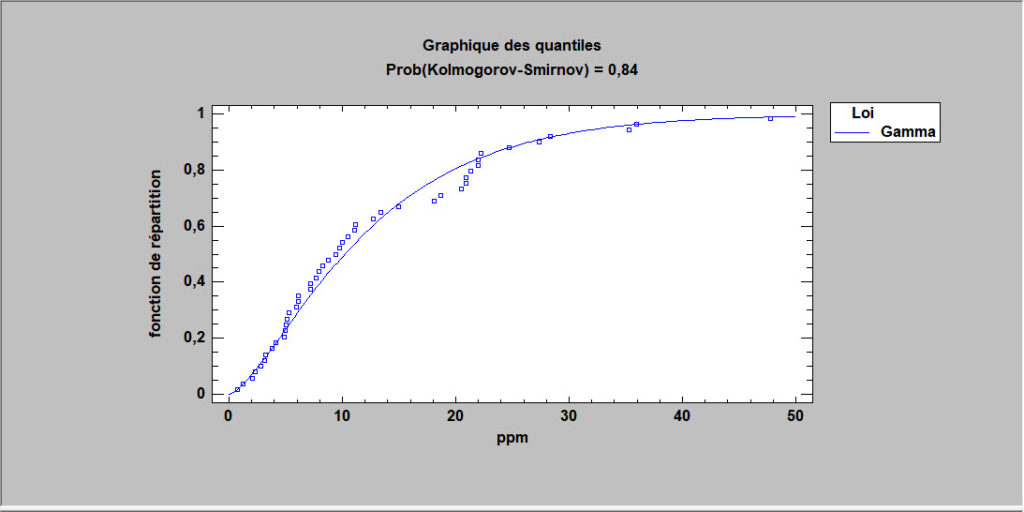
Tests d’adéquation

Les tests d’adéquation sont utilisés pour comparer la fréquence d’occurrence des observations (qu’elles soient quantitatives ou qualitatives) à un modèle probabiliste. Ces tests spécifiques comprennent le test d’adéquation du khi carré, le test de Kolmogorov-Smirnov et le test d’Anderson-Darling.

Un unique échantillon ou deux échantillons appariés

Lorsque les données sont collectées auprès d’une seule population ou sous forme d’échantillons appariés de deux populations, il est souvent nécessaire d’estimer et de tester les paramètres de ces populations. La procédure d’analyse à une variable teste la valeur de la médiane d’une population ou la différence entre les deux médianes à l’aide d’un test de signe ou d’un test de rang signé. Elle calcule également des estimations des intervalles de la moyenne, de l’écart type et de la médiane à l’aide de la méthode bootstrap, une technique dans laquelle les estimations sont obtenues en créant de nombreux nouveaux échantillons à partir des valeurs des données observées.

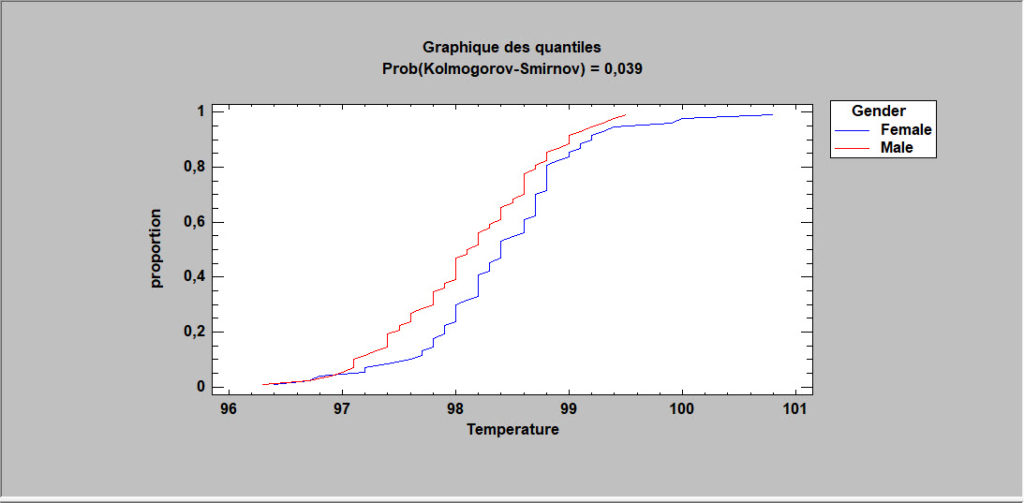
Comparaison de deux échantillons

Lorsque les données sont collectées à partir de deux populations en prenant des échantillons indépendants, des tests statistiques peuvent être calculés sans supposer que les observations des populations sont normalement distribuées. La procédure de comparaison de deux échantillons exécute un test de Mann-Whitney (Wilcoxon) pour comparer les médianes et un test bilatéral de Kolmogorov-Smirnov pour comparer les lois.

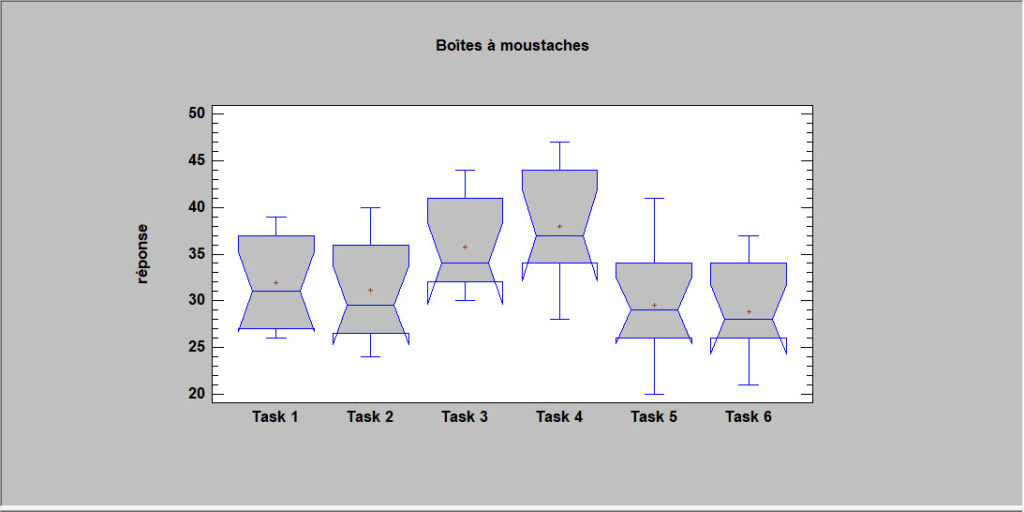
Comparaison de plusieurs échantillons

Lorsque les données sont collectées à partir de plus de deux populations, la procédure de comparaison de plusieurs échantillons peut tester les différences significatives entre les médianes des populations à l’aide du test de Kruskal-Wallis, du test de Mood sur les médianes ou du test de Friedman. Elle peut également afficher des boîtes à moustaches avec encoches, qui ont la propriété que si deux échantillons ont des encoches sur les médianes qui ne se chevauchent, alors il y a une différence statistiquement significative entre les médianes des populations respectives.

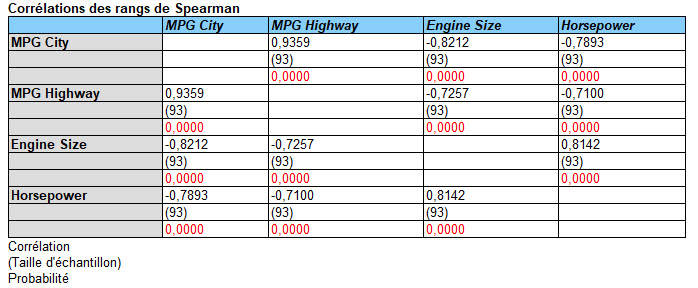
Matrice des corrélations

La procédure d’analyse de plusieurs variables calcule les corrélations entre les paires de variables à l’aide des coefficients de corrélation de Pearson ou les coefficients de corrélation des rangs de Kendall ou de Spearman.

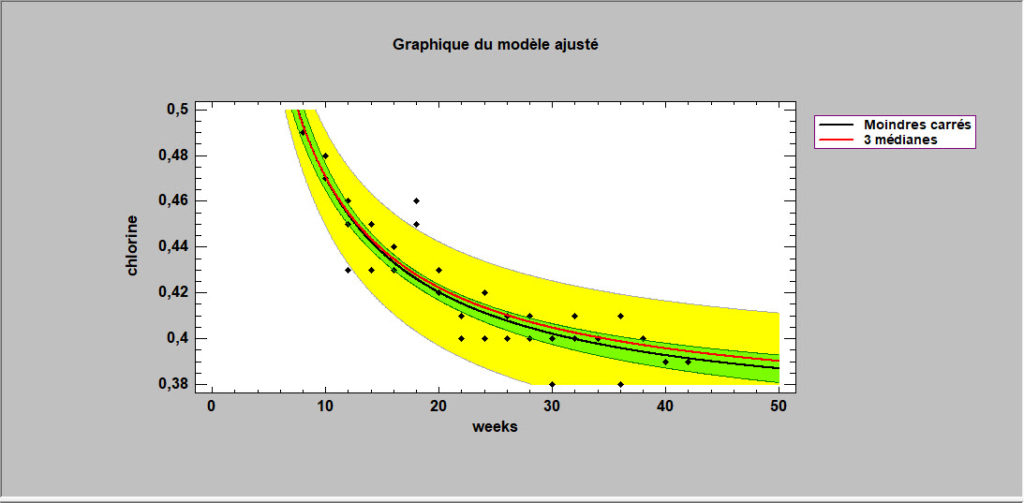
Ajustement de courbes

La procédure de régression simple fournit deux alternatives aux moindres carrés pour ajuster les courbes linéaires et non linéaires reliant Y et X. Celles-ci incluent la minimisation de la somme des écarts absolus autour de la courbe ajustée et la méthode de Tukey consistant à utiliser les médianes de trois groupes.

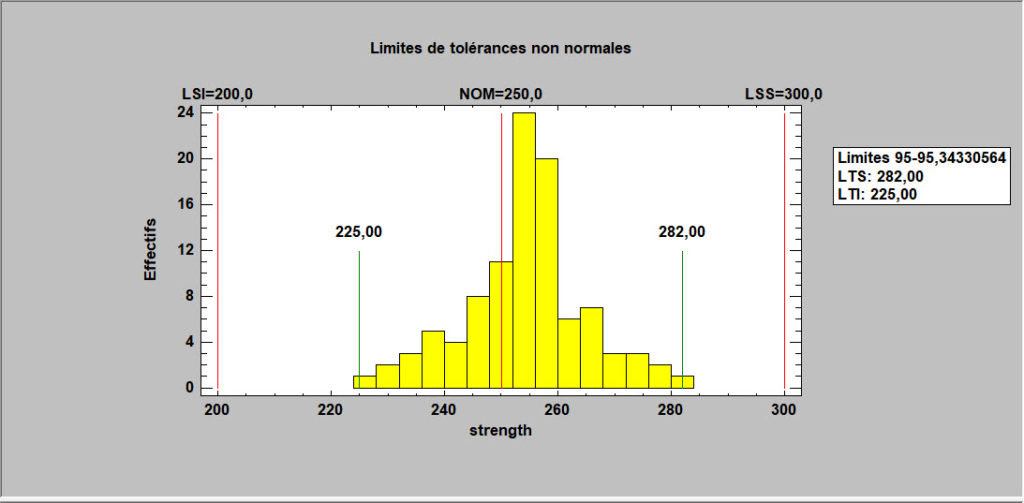
Limites de tolérances non paramétriques

Les limites de tolérances statistiques définissent une plage de valeurs pour X telle que l’on peut être sûr à 100(1-alpha) % que P % de la population dont provient un échantillon de données se situe dans cette plage. Les limites non paramétriques ne supposent pas que les données proviennent d’une distribution particulière. Cependant, ils ne sont pas aussi précis ou aussi flexibles que ceux basés sur l’hypothèse d’une distribution spécifique.

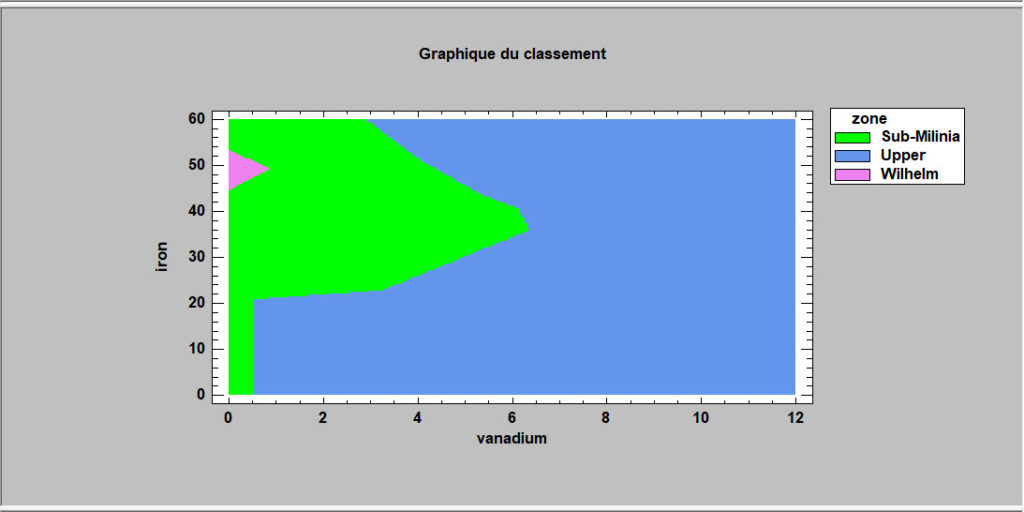
Réseaux de neurones

Cette procédure met en œuvre une méthode non paramétrique de classement d’observations dans un groupe parmi g en se basant sur p variables quantitatives observées. Plutôt que de faire des hypothèses sur la nature de la distribution des variables dans les groupes, elle calcule une estimation non paramétrique des fonctions de densité de chacun des groupes en un point donné en se basant sur les observations voisines dans le groupe. Cette estimation est élaborée en utilisant une fenêtre de Parzen qui pondère les observations de chaque groupe en fonction de la distance au point donné. Les observations sont affectées aux groupes en fonction de trois critères : la fonction de densité estimée au voisinage du point, les probabilités initiales d’appartenance aux groupes et les coûts des erreurs de classements. La sphère d’influence de la fonction de pondération de Parzen peut être définie par l’utilisateur ou évaluée par la méthode jackknife.

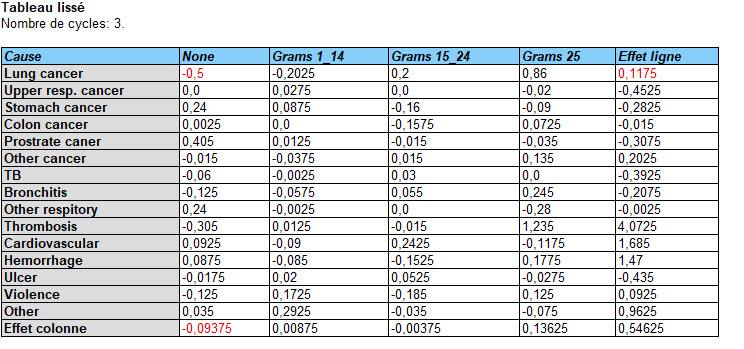
Lissage par la médiane

Cette procédure a pour but d’identifier les formes dans un tableau de données à deux entrées. Elle le fait en exprimant chaque cellule du tableau comme la somme d’une valeur commune, d’un effet ligne, d’un effet colonne et d’un résidu. Cette procédure est similaire à une analyse de la variance à deux facteurs sauf qu’elle base les estimations des effets sur les médianes plutôt que sur les moyennes.

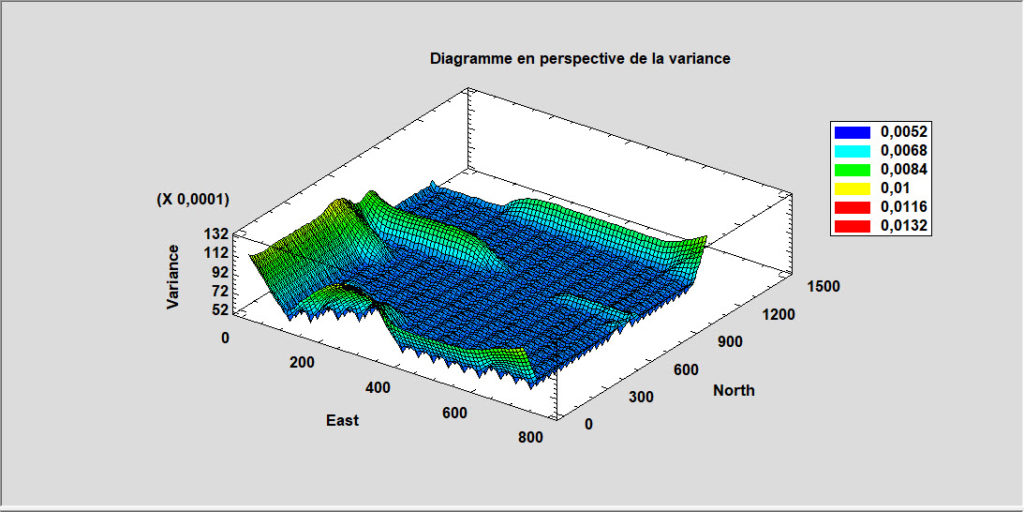
Krigeage

Le krigeage est une technique largement utilisée pour analyser des données géospatiales. A partir d’un ensemble de mesures d’une variable à différentes positions dans une région à deux dimensions, des estimations sont calculées pour la valeur de cette variable dans toute cette région. Les principaux résultats sont des cartes des valeurs estimées et de la variance de ces estimations.