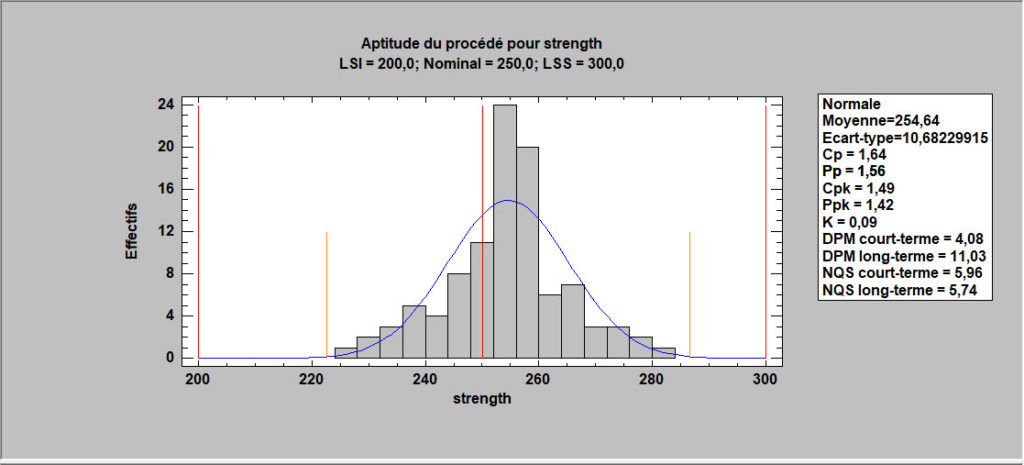
Analyse d’aptitude pour des données normales

Cette procédure effectue une analyse d’aptitude pour les données supposées être un échantillon aléatoire d’une distribution normale. Il calcule des indices d’aptitude tels que Cpk, estime le DPM (défauts par million) et détermine le niveau de qualité sigma (SQL) auquel le processus fonctionne. Il peut gérer les limites de spécification symétriques bilatérales, les limites asymétriques bilatérales et les limites unilatérales. Des limites de confiance pour les indices d’aptitude les plus courants peuvent également être demandées.

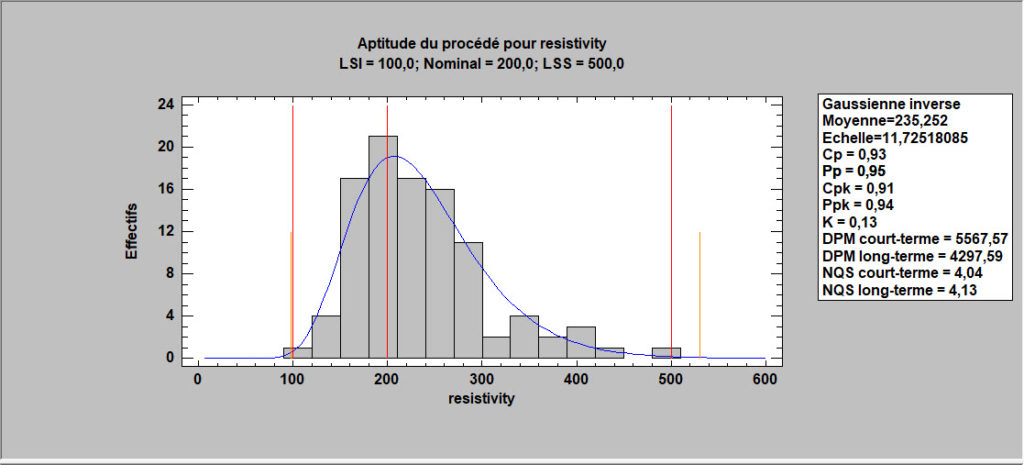
Analyse d’aptitude pour des données non normales

Cette procédure effectue une analyse d’aptitude pour les données qui ne sont pas supposées provenir d’une distribution normale. Le programme ajuste jusqu’à 25 distributions alternatives et les liste en fonction de leur adéquation. Pour une distribution sélectionnée, il calcule ensuite les indices d’aptitude équivalents, le DPM et le SQL.

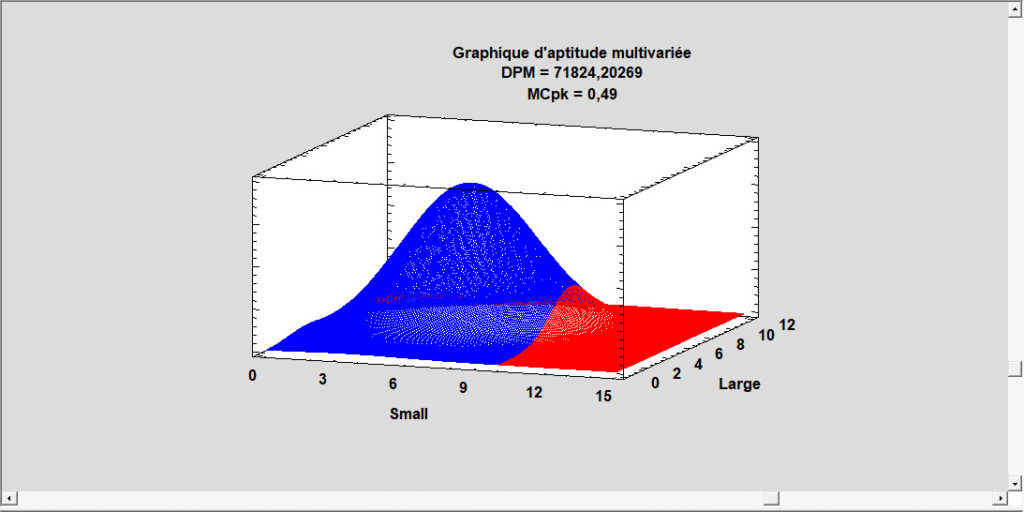
Analyse d’aptitude pour des données corrélées

Lorsque les variables qui caractérisent un processus sont corrélées, l’estimation séparée de l’aptitude de chacune peut donner une image très déformée de la performance du processus. Dans de tels cas, il est nécessaire d’estimer la probabilité conjointe qu’une ou plusieurs variables soient hors spécifications. Cela nécessite l’ajustement d’une distribution de probabilité multivariée. Cette procédure calcule les indices d’aptitude, le DPM et le SQL sur la base d’une distribution normale multivariée.

Analyse d’aptitude pour des comptages ou des proportions

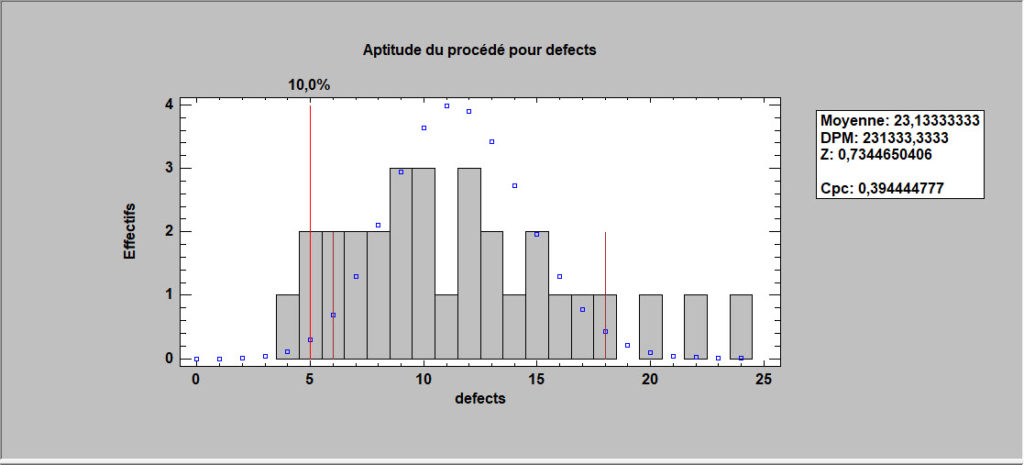
Lorsque l’examen d’un élément ou d’un événement aboutit à une BON ou à un MAUVAIS plutôt qu’à une mesure, l’analyse de l’aptitude du processus doit être basée sur une distribution discrète. Pour les très grands lots, la distribution pertinente est le loi binomiale. Pour les petits lots ou les cas d’opportunités limitées d’échec, la distribution hypergéométrique doit être utilisée.

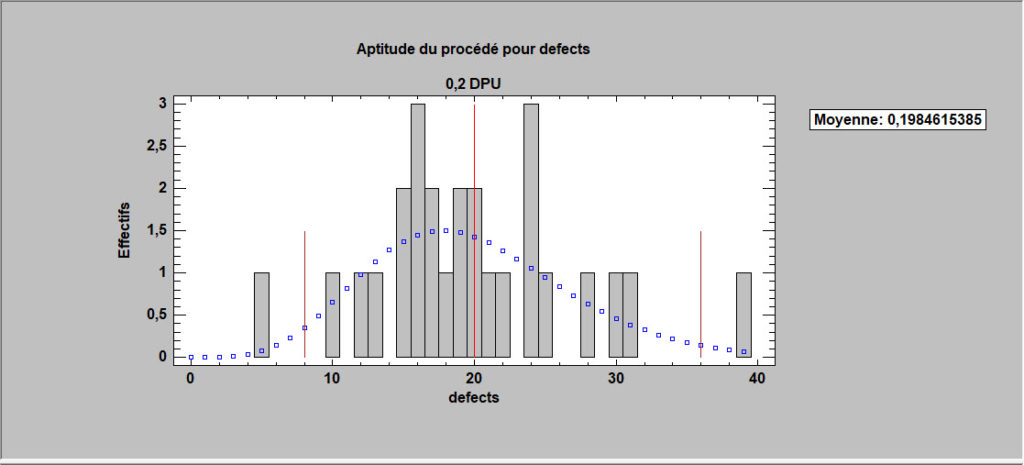
Analyse d’aptitude pour des taux

Lorsque la mesure de performance pertinente est un taux (défauts par unité), l’analyse d’aptitude du processus est basée sur une distribution de Poisson si la variance est approximativement égale à la moyenne ou sur une distribution binomiale négative si la variance est plus grande que la moyenne.

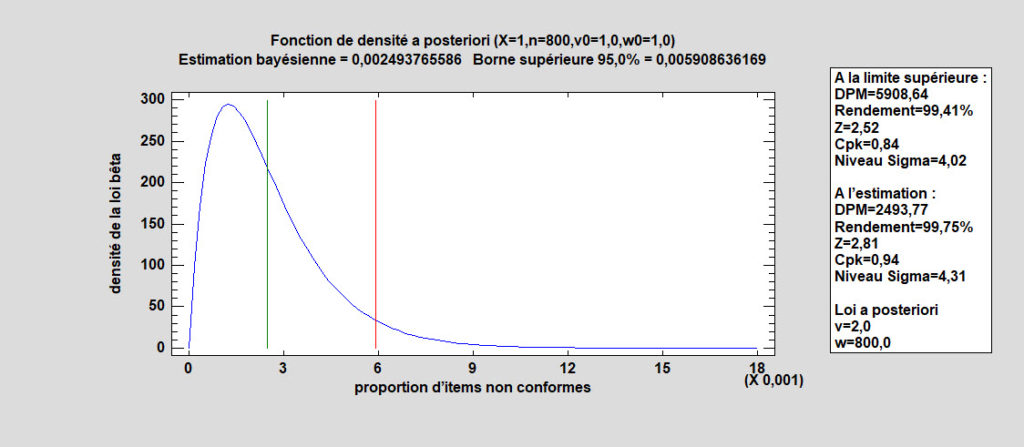
Estimation bayésienne de l’aptitude

Lorsqu’il existe des connaissances préalables sur la proportion probable d’éléments non conformes générés par un processus, une approche bayésienne de l’estimation de l’aptitude du processus peut donner des estimations plus précises que si l’on utilise uniquement un nouvel échantillon de données. La combinaison des connaissances antérieures avec les données actuelles crée une distribution a posteriori qui peut être utilisée pour obtenir une estimation ponctuelle et  un intervalle de l’aptitude du processus.

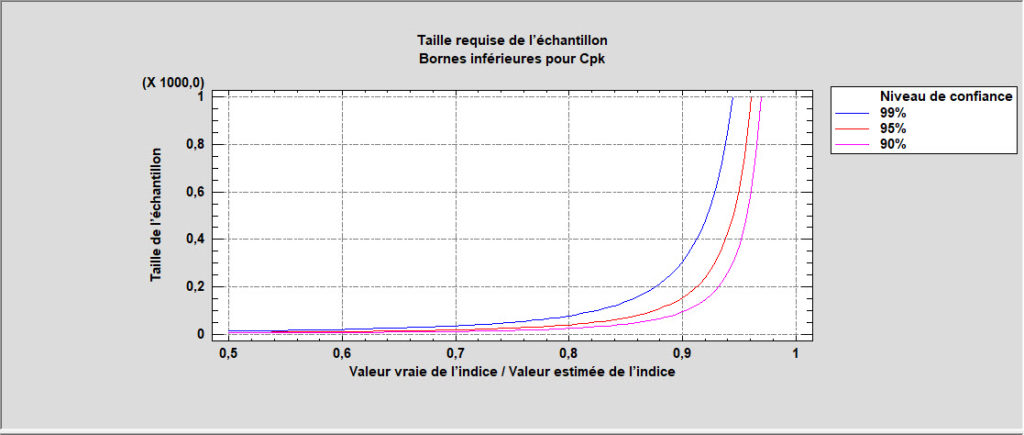
Détermination de la taille d’un échantillon pour estimer des indices d’aptitude

Cette procédure détermine une taille d’échantillon appropriée pour estimer trois indices d’aptitude : Cp, Cpk et Cpm. La détermination est basée soit sur la précision souhaitée de l’estimation, soit sur la puissance d’un test d’hypothèse.