Tables de survie

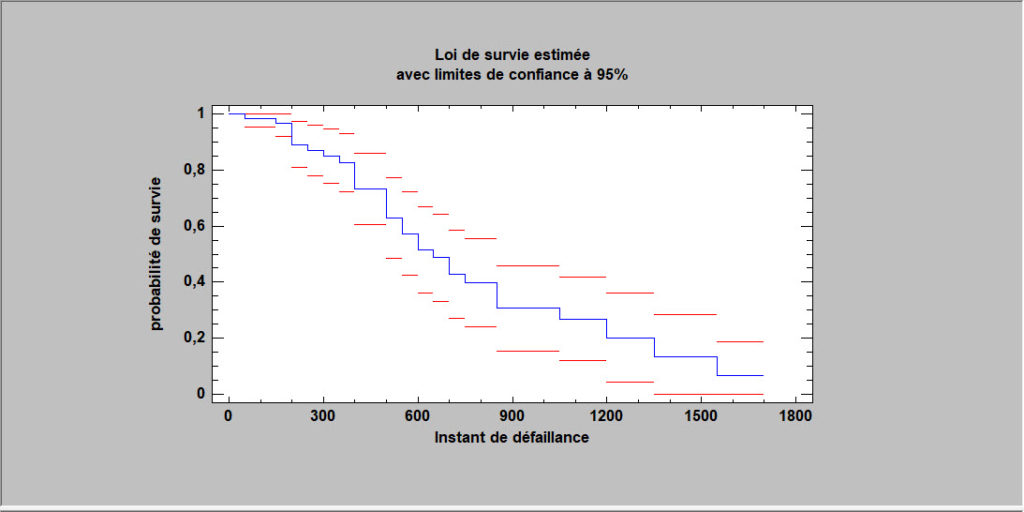
Dans l’analyse des données de durée de vie, l’intérêt se concentre généralement sur l’estimation de la probabilité qu’une unité soit encore en fonctionnement à un moment donné. Une façon courante d’estimer cette fonction de survie, sans faire aucune hypothèse sur la forme fonctionnelle ou la distribution des erreurs, consiste à tabuler les données et à calculer la fonction de survie directement à partir des défaillances observées à l’aide d’outils d’analyse des défaillances. Lorsque la censure est présente, les estimations sont calculées à l’aide de l’approche de Kaplan-Meier.

Ajustement de lois à des données censurées

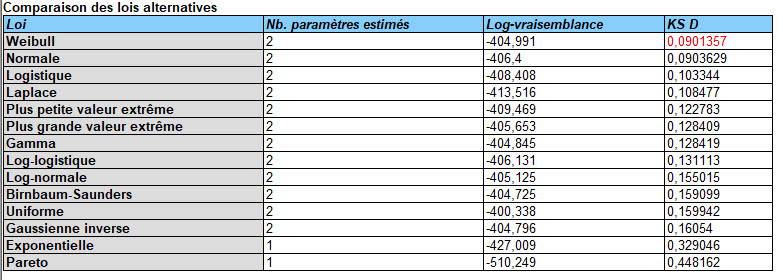
Si suffisamment de données sont disponibles, il peut être possible, en utilisant les bons outils d’analyse des défaillances, d’ajuster une loi spécifique aux temps de défaillance. Les méthodes du maximum de vraisemblance peuvent être facilement adaptées à la présence de données censurées. STATGRAPHICS ajustera automatiquement jusqu’à 45 lois de probabilité à tout échantillon de données durant l’analyse des données de survie et les classera en fonction de la qualité de l’ajustement.

Analyse de Weibull

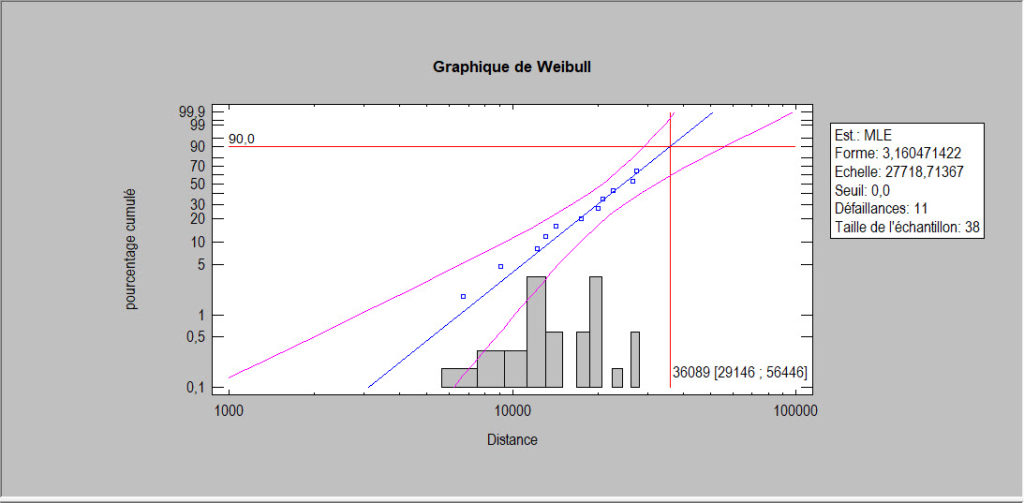
L’expérience a montré que les données issues de l’analyse des données de survie peuvent souvent être bien modélisées par une loi de Weibull. Une méthode courante pour vérifier l’ajustement d’une loi de Weibull consiste à utiliser un graphique de Weibull. Les temps de défaillance non censurés doivent s’aligner approximativement le long d’une ligne droite. Avec les outils d’analyse des défaillances de STATGRAPHICS, vous pouvez ajouter un histogramme des temps de défaillance censurés et des limites de confiance pour les centiles de défaillance au diagramme de Weibull.

Graphiques de tests de durée de vie accélérés

Lorsque les pannes ne se produisent pas assez souvent dans des conditions normales de fonctionnement, il est nécessaire d’accélérer les pannes en augmentant la contrainte causée par une ou plusieurs variables. Un accélérateur très courant est la température. En analysant les taux de défaillance à haute température et en ajustant un modèle d’Arrhenius, il est souvent possible d’extrapoler les données à une température de fonctionnement normale (généralement exprimée en Kelvin).

Cette procédure permet d’ajuster d’ajuster six modèles différents d’accélération, pas uniquement le modèle d’Arrhenius : Arrhenius, règle de la puissance inverse, exponentiel, Eyring, linéaire, réciproque.

Elle permet la conversion automatique en degrés Kelvin si les données ont été saisies en degrés Celsius.

Régression sur données de survie

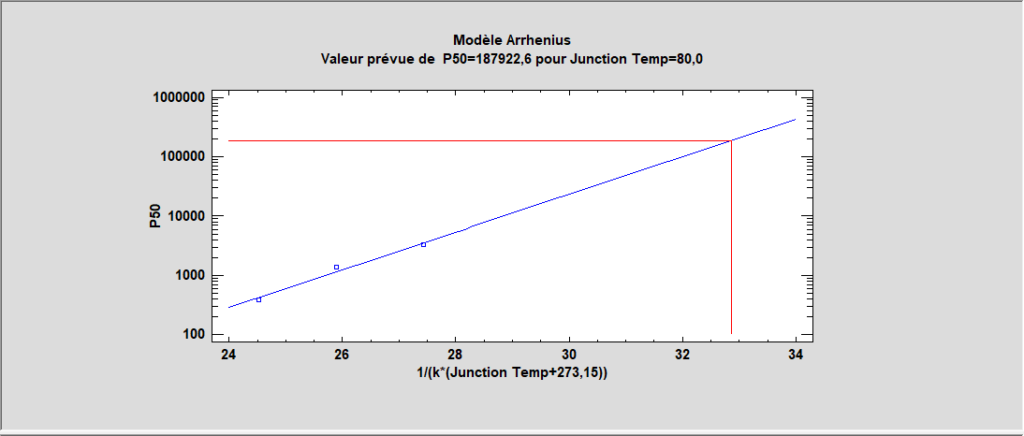
Pour décrire l’impact des variables externes sur les temps de défaillance, des modèles de régression peuvent être adaptés. Malheureusement, les techniques standard des moindres carrés ne fonctionnent pas bien pour deux raisons : les données sont souvent censurées (à gauche, à droite ou par intervalles) et la distribution des temps de défaillance est rarement gaussienne. Pour cette raison, STATGRAPHICS fournit une procédure spéciale avec des outils d’analyse des défaillances qui ajusteront les modèles de régression sur des données de survie avec censures, en supposant une distribution exponentielle, valeur extrême, logistique, log-logistique, log-normale, normale ou de Weibull. Le graphique de la loi des temps des défaillances est affiché ainsi que la durée moyenne avant défaillance (MTTF) et les quantiles..

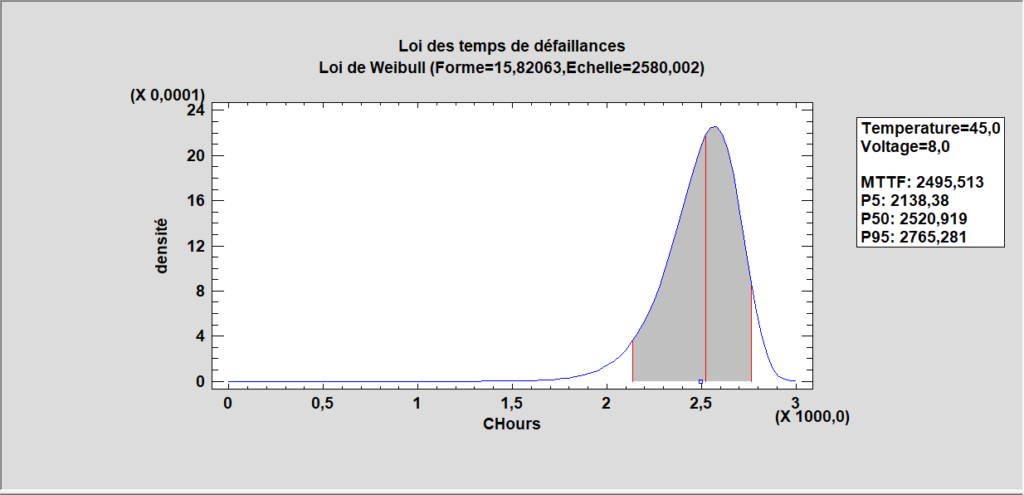
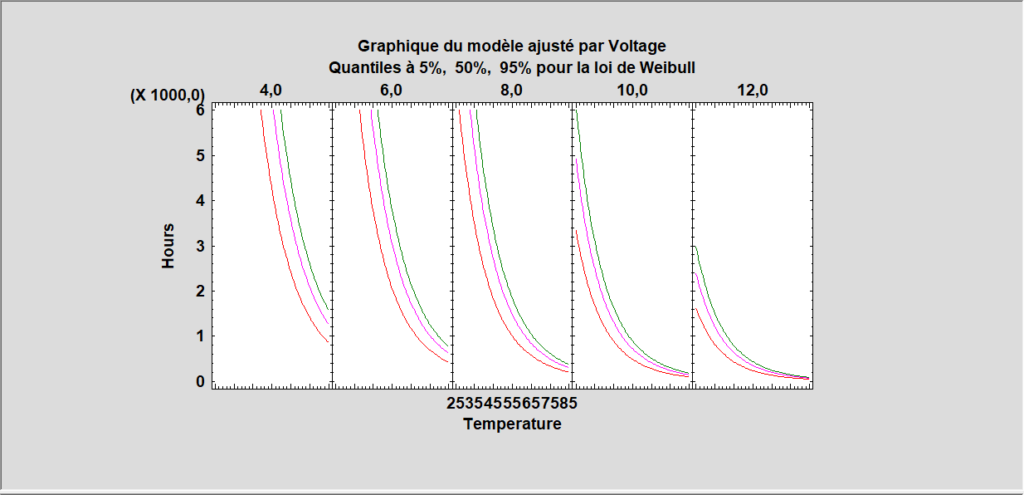
Tests de durée de vie accélérés

Cette procédure utilise des données de temps de défaillances et/ou de censures et ajuste des modèles de régression similaires à ceux de la procédure « Régression sur données de survie ». Les principales différences avec cette procédure sont :

Il doit y avoir au moins un facteur d’accélération quantitatif qui est supposé suivre l’un des six modèles d’accélération listés ci-dessus.

Des variables quantitatives et qualitatives supplémentaires peuvent être ajoutées au modèle comme termes linéaires.

La loi des temps des défaillances peut prendre sept formes différentes : Weibull, exponentielle, normale, log-normale, logistique, log-logistique ou plus petite valeur extrême. Les lois disponibles dépendent du modèle d’accélération sélectionné.

Des graphiques sont créés pour chaque valeur observée du facteur d’accélération.

A noter que les données utilisées sont les temps observés des défaillances ou des censures et non les quantiles comme dans la procédure « Graphiques de tests de durée de vie accélérés ».

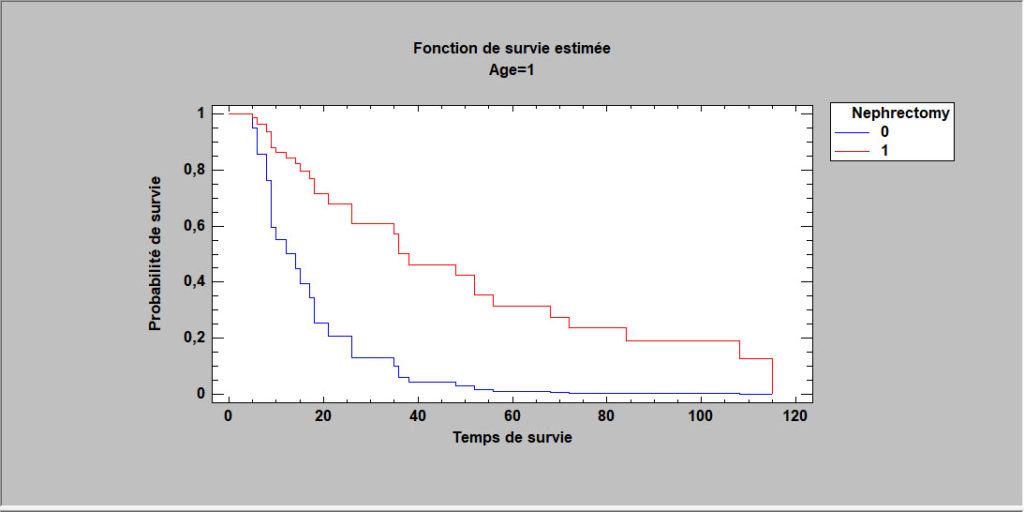
Risques proportionnels de Cox

Cette La procédure est conçue pour ajuster un modèle semi-paramétrique reliant des temps de défaillances à une ou plusieurs variables explicatives. Les variables explicatives peuvent être quantitatives ou qualitatives. Des modèles du premier ordre et du second ordre peuvent être ajustés, avec ou sans interactions. A la différence de la procédure Régression sur données de survie, aucune hypothèse n’est faite sur la loi des temps de défaillances. La seule hypothèse est que les variables explicatives agissent de façon multiplicative sur la fonction de risque. Les temps de défaillances peuvent être censurés ou non censurés.

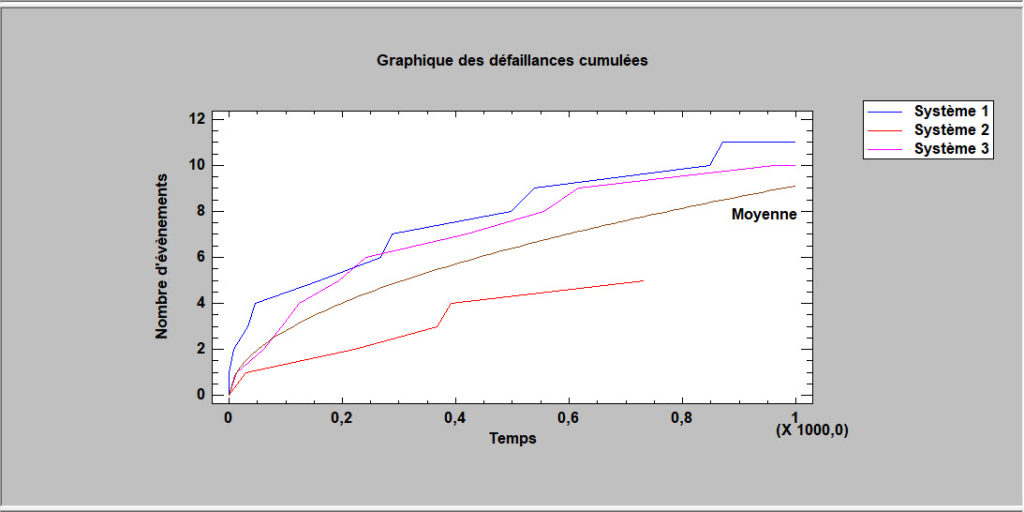
Analyse de systèmes réparables

Les analyses de systèmes réparables sont conçues pour étudier les données constituées des temps de défaillance de systèmes qui peuvent être réparés. On suppose que lorsque le système tombe en panne, il est immédiatement réparé et remis en service. De plus, on suppose que le temps de réparation est négligeable par rapport au temps entre les pannes. Le but de l’analyse est de développer un modèle qui peut être utilisé pour estimer les taux de défaillance ou des quantités telles que le MTBF (temps moyen entre les défaillances). Cette procédure d’analyse des données de durée de survie diffère des procédures d’ajustement de lois et de l’analyse de Weibull en ce qu’elle permet un taux d’échec qui change à mesure que le système vieillit.

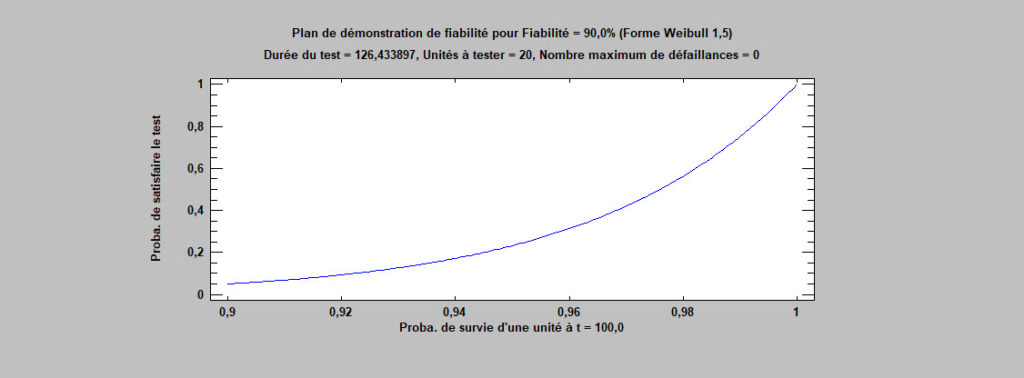
Plans de démonstration de fiabilité

Cette procédure crée des plans de test pour démontrer qu’une loi de temps de défaillances satisfait des conditions données. Par exemple, il peut être souhaité montrer, avec un niveau de confiance de 95%, que la fiabilité d’un produit est supérieure ou égale à 90% à la fin de la période de garantie. Durant la démonstration, n unités seront testées pendant une durée t. La démonstration sera considérée comme satisfaisante si pas plus de f unités ont eu une défaillance durant le test. L’utilisateur précise soit le nombre d’unités à tester, soit la durée du test. La procédure calcule les autres quantités.