Lois de probabilités

Cette procédure permet d’effectuer diverses opérations sur 51 lois de probabilités. En particulier, vous pouvez afficher le graphique de la fonction de masse ou de densité, des fonctions de répartition et de survie, du log de la fonction de survie et de la fonction de risque, calculer des aires sous la courbe et des valeurs critiques et générer des nombres aléatoires.

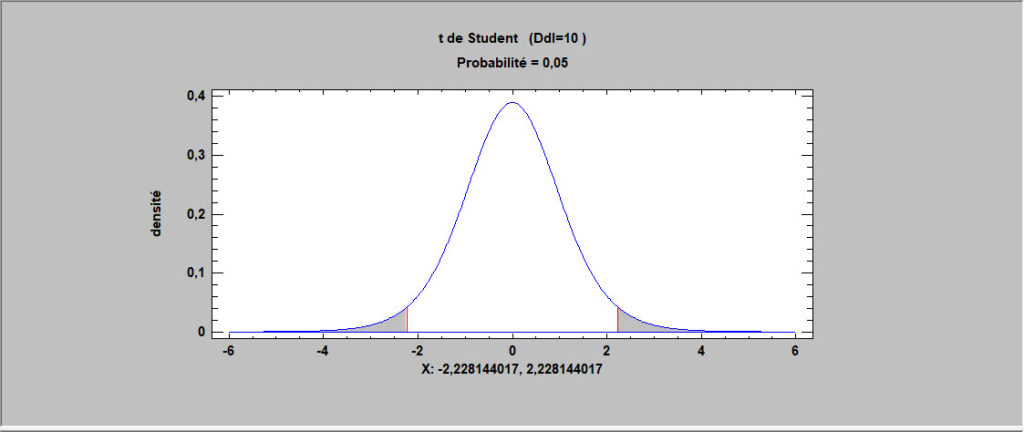
Distributions d’échantillonnage

Cette procédure calcule des aires sous la courbe et des valeurs critiques pour quatre distributions d’échantillonnage courantes : loi normale, loi du t de Student, loi du khi-carré et loi F du rapport des variances. Elle affiche également les résultats sous forme graphique.

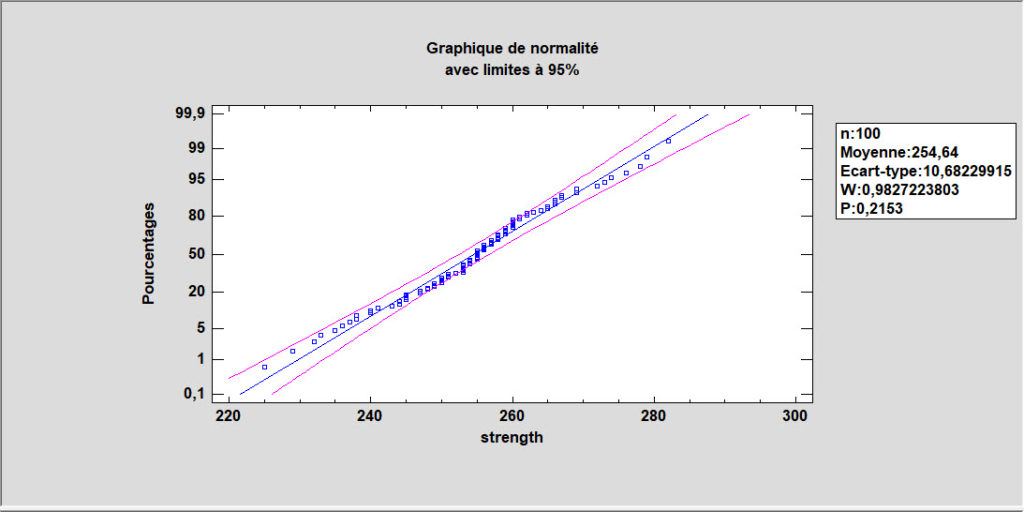
Graphique de normalité

Le graphique de normalité est utilisé pour aider à déterminer si un échantillon de données numériques provient ou non d’une loi normale. Si ce n’est pas le cas, vous pouvez fréquemment déterminer le type d’écart à la normalité en examinant la façon dont les données s’écartent de la ligne de référence normale.

Graphiques de lois de probabilités non normales

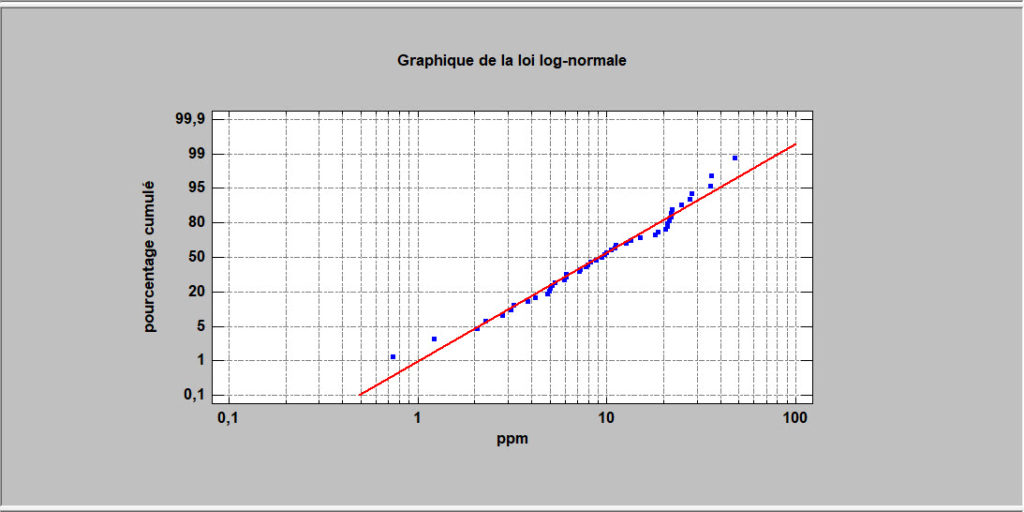
Cette procédure affiche les données d’une colonne numérique sous la forme de graphiques qui sont spécifiquement mis à l’échelle de sorte que, si les données proviennent d’une distribution particulière, les observations s’aligneront approximativement le long d’une ligne droite. La procédure comprend des tracés pour les lois uniforme, normale, log-normale, Weibull, plus petite valeur extrême, logistique et exponentielle.

Ajustement de lois (données non censurées)

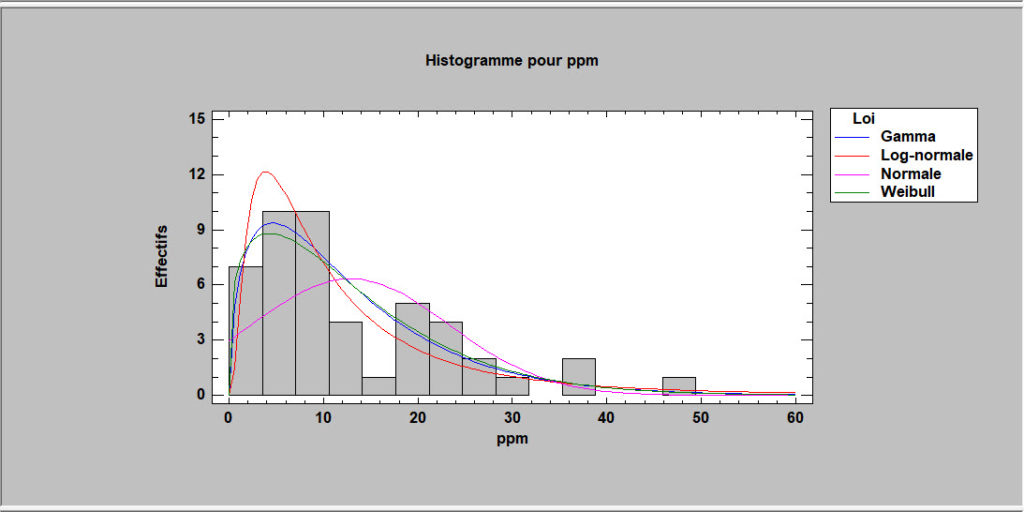
Cette procédure ajuste l’une des 48 lois de probabilités à une colonne de données numériques. Les données sont supposées non censurées, c’est-à-dire qu’elles représentent des échantillons aléatoires de la loi sélectionnée. Si les données ont été censurées à cause d’une limite de détection ou pour une autre cause, il faut utiliser la procédure Ajustement de lois (données censurées).

Ajustement de lois (données censurées)

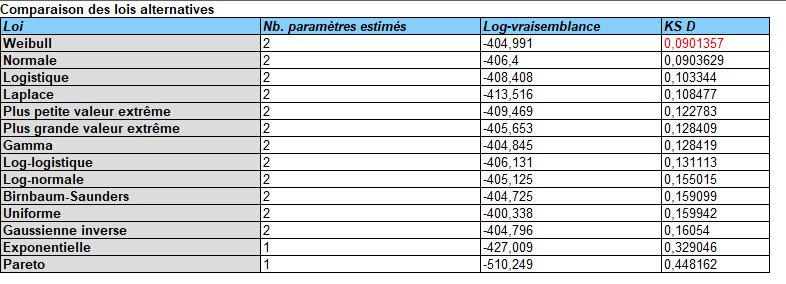
Cette procédure permet d’ajuster 48 lois de probabilités à une colonne de données numériques censurées. La censure survient lorsque quelques-unes des données ne sont pas connues exactement. Par exemple, lors de la mesure de temps de défaillances, certains objets de l’étude peuvent ne pas avoir subi de défaillances lorsque l’étude est terminée. Cela donne des bornes inférieures des temps de défaillances pour ces objets.

Ajustement de lois (données censurées arbitrairement)

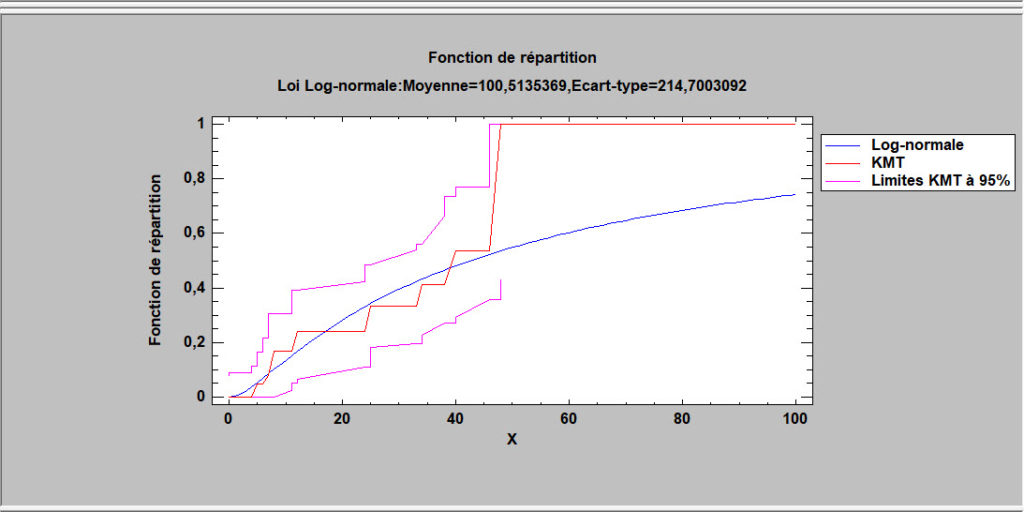
Cette procédure analyse des données dans lesquelles une ou plusieurs observations ne sont pas connues de façon exacte. En particulier, les observations peuvent être censurées à gauche (inférieures à une valeur donnée), censurées à droite (supérieures à une valeur donnée), censurées par intervalle (comprises dans un intervalle donné). La procédure calcule des statistiques descriptives, ajuste des lois de probabilités, crée des graphiques et calcule une estimation non paramétrique de la fonction de survie.

Génération de nombres aléatoires

Des nombres aléatoires peuvent être générés par le logiciel pour chacune des lois de probabilité en utilisant cette procédure. Ils peuvent également être générés dans le cadre des simulations Monte-Carlo.

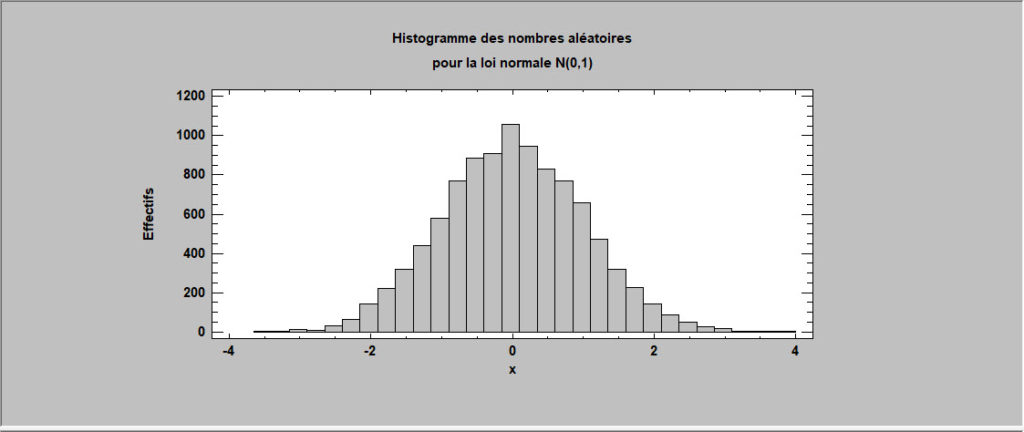
Nombres aléatoires pour un loi normale multivariée

Cette procédure génère des nombres aléatoires pour une loi normale multivariée pouvant utiliser jusqu’à 12 variables. L’utilisateur entre les moyennes, écarts-types des variables ainsi que la matrice des corrélations. Les échantillons aléatoires générés peuvent être enregistrés dans le classeur de Statgraphics.

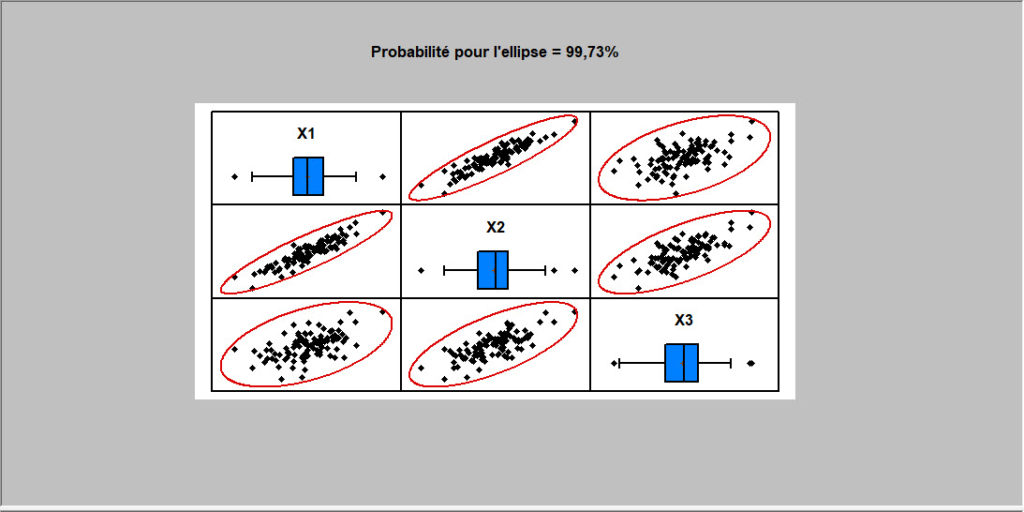
Limites statistiques de tolérances

Les limites de tolérance statistique délimitent une proportion donnée d’une population à un niveau de confiance spécifié. Ils ont de nombreuses utilisations, notamment pour démontrer qu’une grande partie des échantillons d’une population se situent dans les limites requises. Statgraphics Centurion calcule des limites de tolérance statistiques pour 11 lois de probabilités ainsi que des limites non paramétriques.

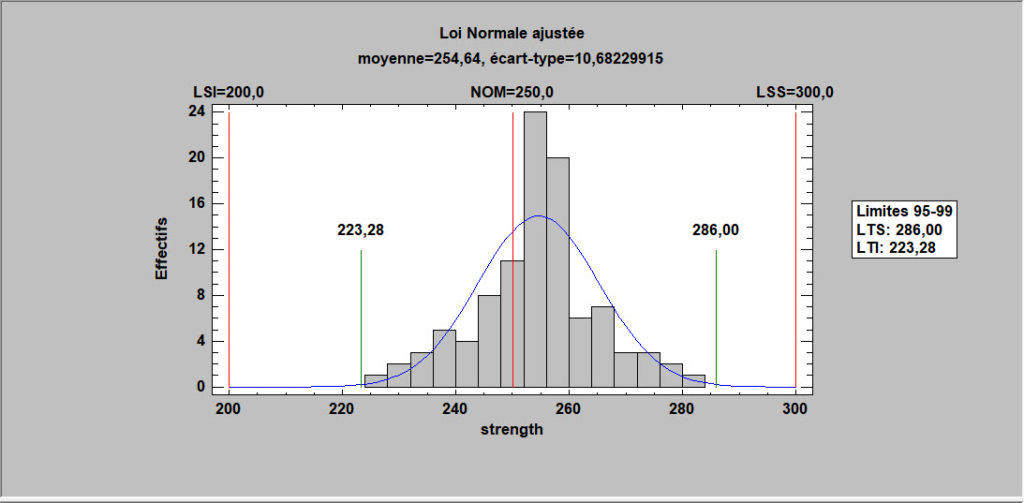
Limites de tolérances multivariées

Cette procédure affiche des limites de tolérances pour des données constituées de plus d’une variable. Elle affiche une région des tolérances qui contient un pourcentage donné p de la population avec un niveau de confiance de 100(1-alpha)%. Elle inclut également des limites simultanées des tolérances pour chaque variable en utilisant l’approche de Bonferroni. Les données sont supposées être un échantillon aléatoire provenant d’une loi normale multivariée. Les limites de tolérances multivariées sont souvent comparées aux limites de spécifications pour plusieurs variables pour déterminer si la plus grande partie de la population est à l’intérieur des spécifications.

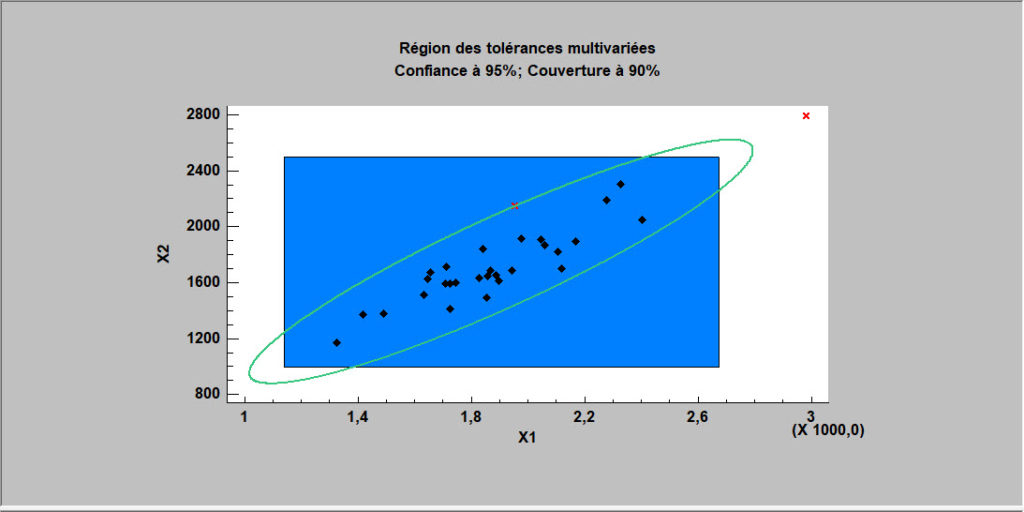
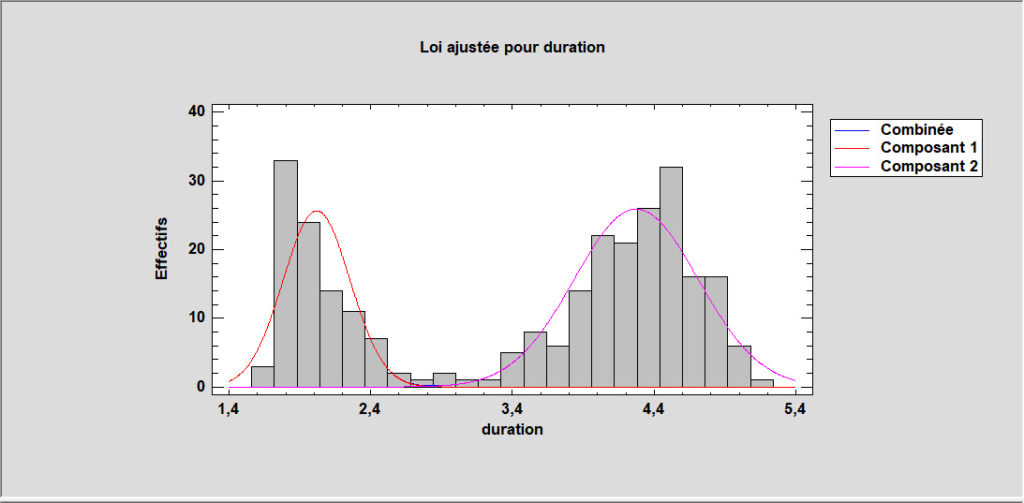
Modèles de mélanges univariés

Cette procédure ajuste une loi à des données numériques continues qui sont constituées d’un mélange de deux lois gaussiennes univariées ou plus. Les composants du mélange peuvent représenter différents groupes dans l’échantillon utilisé pour ajuster la loi globale ou le modèle de mélange peut approximer une loi ayant une forme plus complexe. La procédure ajuste la loi, affiche des graphiques et calcule des aires sous la courbe et des valeurs critiques. Des outils sont fournis pour déterminer combien de composants sont nécessaires pour représenter un échantillon de données.

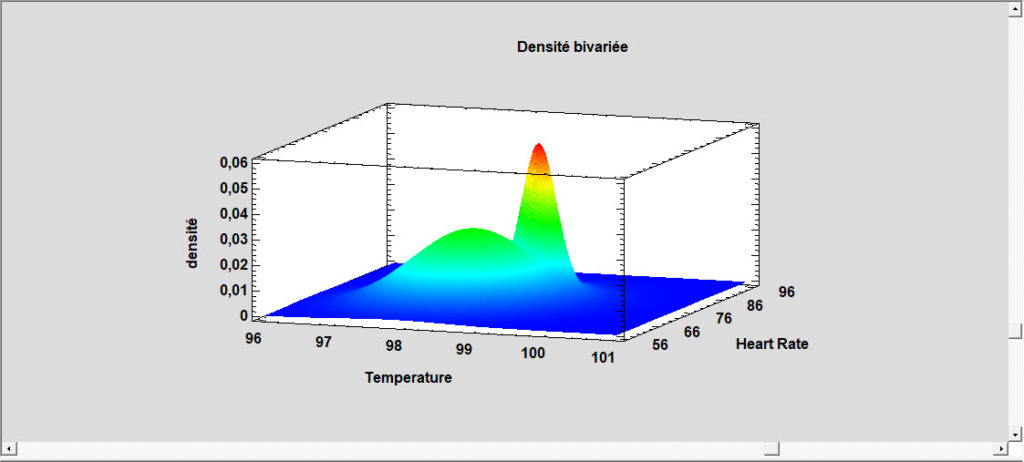
Modèles de mélanges bivariés

Cette procédure ajuste une loi à des données numériques continues qui sont constituées d’un mélange de deux lois gaussiennes bivariées ou plus. Les composants du mélange peuvent représenter différents groupes dans l’échantillon utilisé pour ajuster la loi globale ou le modèle de mélange peut approximer une loi ayant une forme plus complexe. La procédure ajuste la loi, affiche des graphiques et calcule des aires sous la courbe et des valeurs critiques. Des outils sont fournis pour déterminer combien de composants sont nécessaires pour représenter un échantillon de données.