Matrice de nuages de points

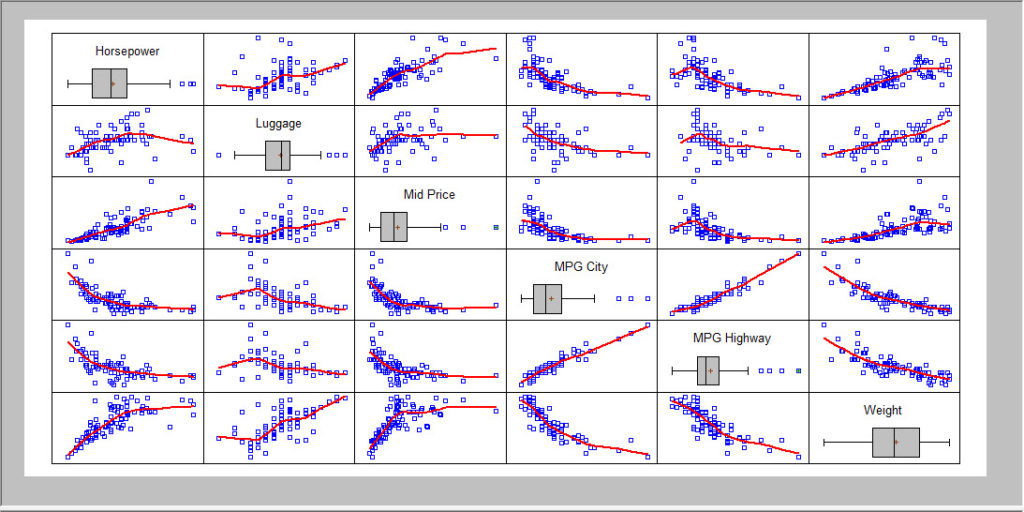
Cette procédure affiche une matrice de nuages de points pour trois variables numériques ou plus. La diagonale de cette matrice est constituée des boîtes à moustaches des différentes variables. La partie hors diagonale contient les nuages de points reliant deux variables pour chaque paire de variables. Cette procédure est très utile pour avoir un premier aperçu de données multivariées. Avec ce graphique, il est souvent possible de détecter des relations entre les variables, la présence de points extrêmes et d’autres caractéristiques intéressantes concernant les données.

Matrice des corrélations

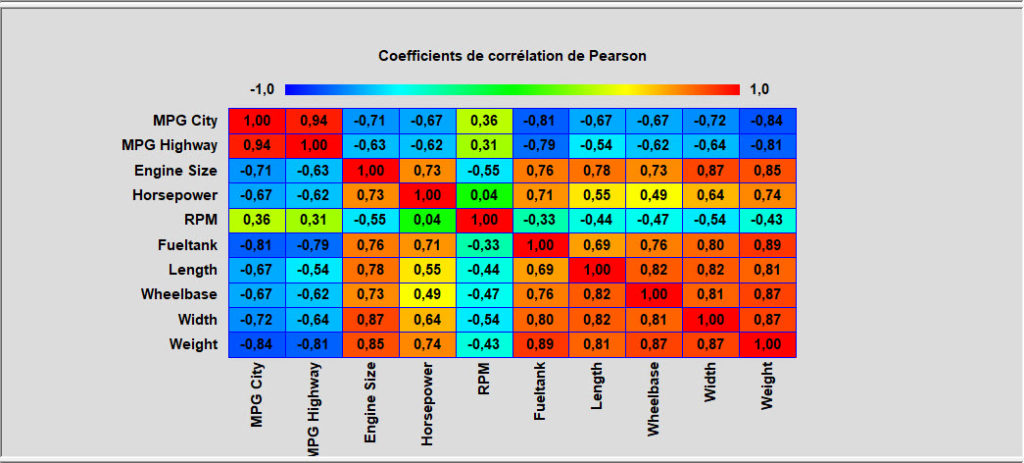
La procédure d’analyse à plusieurs variables est conçue pour résumer deux ou plusieurs colonnes de données numériques. Elle calcule des statistiques résumées pour chaque variable ainsi que les corrélations et les covariances entre les variables. Les graphiques incluent une matrice de nuages de points, des graphiques en étoiles et en rayons de soleil. Cette procédure est souvent utilisée avant de construire un modèle de régression multiple.

Graphique radar

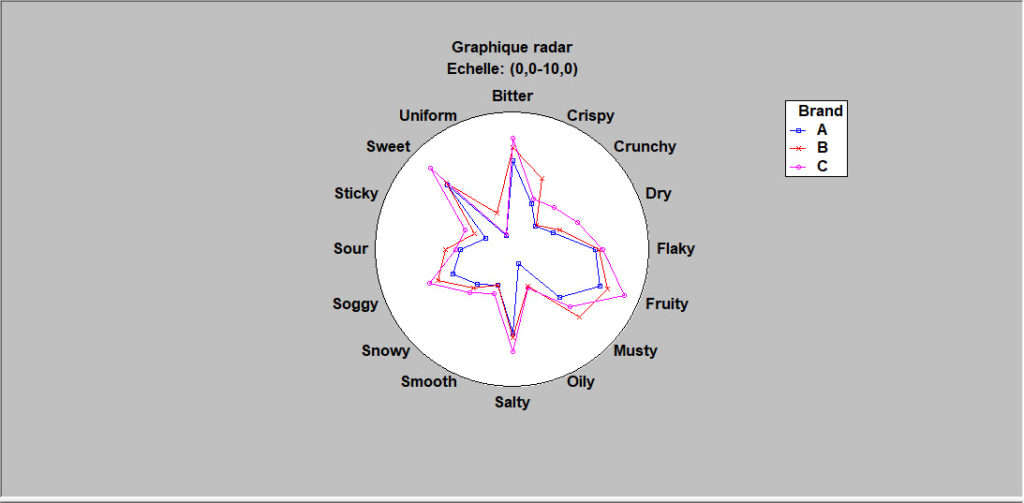
Le graphique radar est utilisé pour illustrer les valeurs de jusqu’à 16 variables pour un petit nombre d’observations. Il est souvent utilisé en analyse sensorielle pour afficher les notes concernant de multiples attributs.

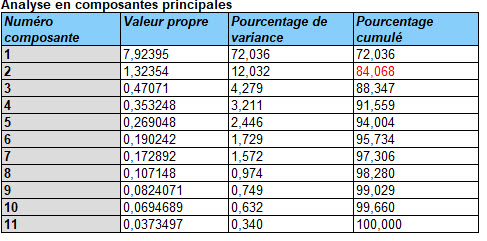
Analyse en composantes principales

Cette procédure est conçue pour extraire des composantes principales d’un ensemble de variables quantitatives X. Les composantes principales sont définies comme l’ensemble des combinaisons linéaires des X qui ont la plus grande variance. Déterminer les composantes principales est souvent utilisé pour réduire la dimensionnalité d’un ensemble de variables prédictrices avant de les utiliser dans des procédures telles que la régression multiple ou la classification.

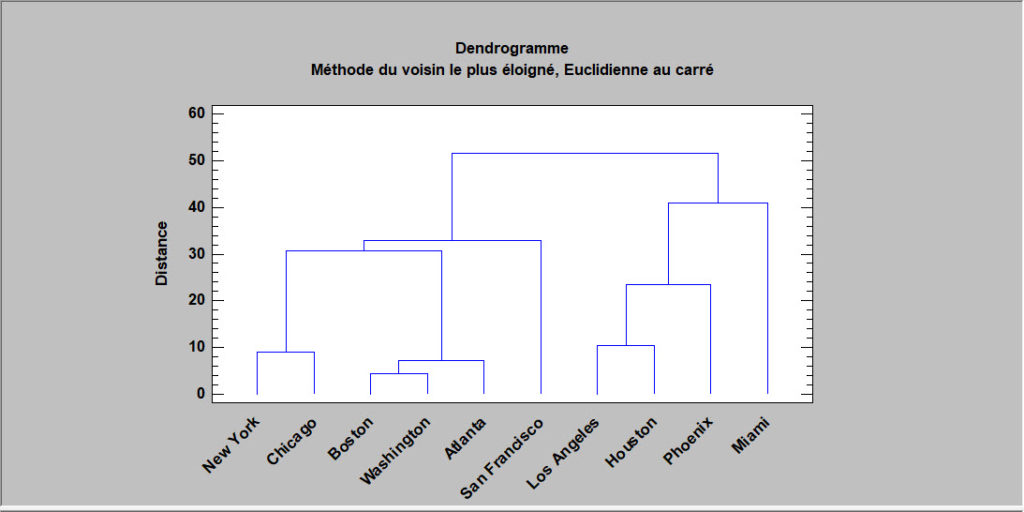
Classification

Une classification regroupe des observations ou des variables en fonction des similitudes entre elles. Le dendrogramme montre les résultats de la procédure de regroupement hiérarchique, qui commence par des observations séparées et les regroupe en fonction de la distance qui les sépare dans un espace multivarié.

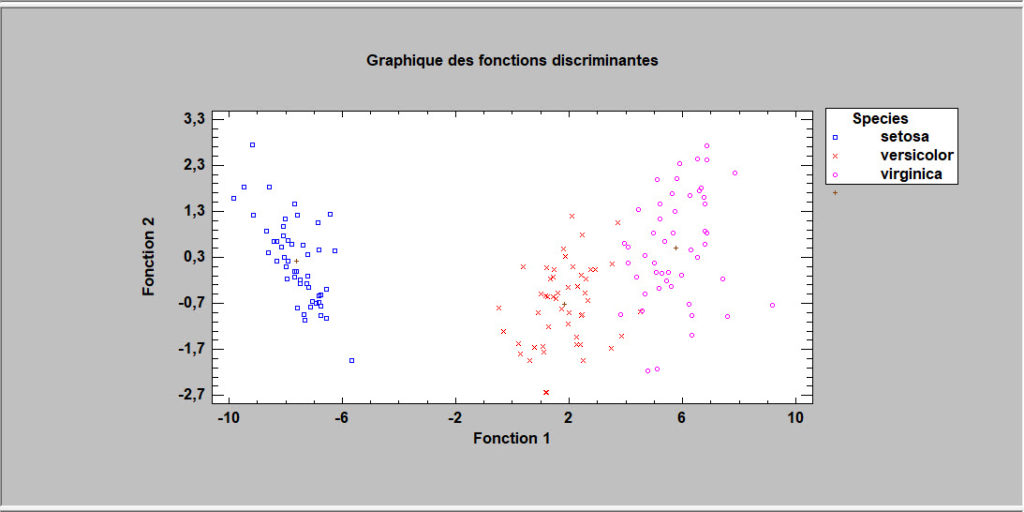
Analyse discriminante

La procédure d’analyse discriminante est conçue pour aider à distinguer deux ou plusieurs groupes de données sur la base d’un ensemble de variables quantitatives observées. Pour ce faire, il construit des fonctions discriminantes qui sont des combinaisons linéaires des variables. L’objectif d’une telle analyse est généralement de décrire mathématiquement les cas observés de manière à les séparer au mieux en groupes et de pouvoir classer les nouvelles observations comme appartenant à l’un ou l’autre des groupes.

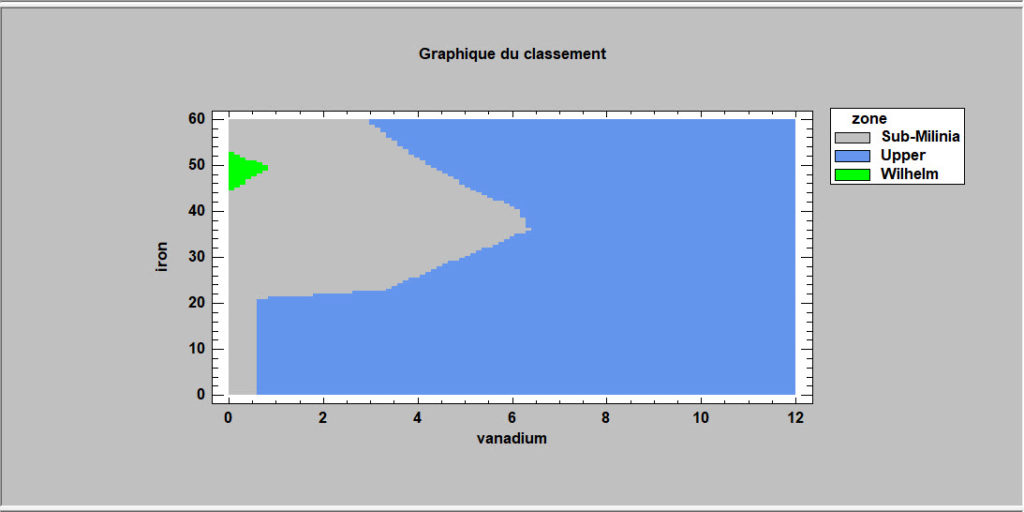
Classement par réseaux de neurones

Cette procédure met en oeuvre une méthode non paramétrique de classement d’observations dans un groupe parmi g en se basant sur p variables quantitatives observées. Plutôt que de faire des hypothèses sur la nature de la distribution des variables dans les groupes, elle calcule une estimation non paramétrique des fonctions de densité de chacun des groupes en un point donné en se basant sur les observations voisines dans le groupe. Cette estimation est élaborée en utilisant une fenêtre de Parzen qui pondère les observations de chaque groupe en fonction de la distance au point donné. Les observations sont affectées aux groupes en fonction de trois critères : fonction de densité estimée au voisinage du point, probabilités initiales d’appartenance aux groupes et coûts des erreurs de classements. La sphère d’influence de la fonction de pondération de Parzen peut être définie par l’utilisateur ou évaluée par la méthode jackknife.

Moindres carrés partiels

Les moindres carrés partiels sont conçus pour construire un modèle statistique reliant plusieurs variables indépendantes X à une ou plusieurs variables dépendantes Y. La procédure est particulièrement utile lorsqu’il existe de nombreux prédicteurs et que l’objectif principal de l’analyse est la prévision des variables de réponse. Contrairement à d’autres procédures de régression, des estimations peuvent être dérivées même dans le cas où le nombre de variables prédictives dépasse le nombre d’observations. La régression PLS est largement utilisée par les ingénieurs chimistes et les chimiométriciens pour l’étalonnage spectrométrique.

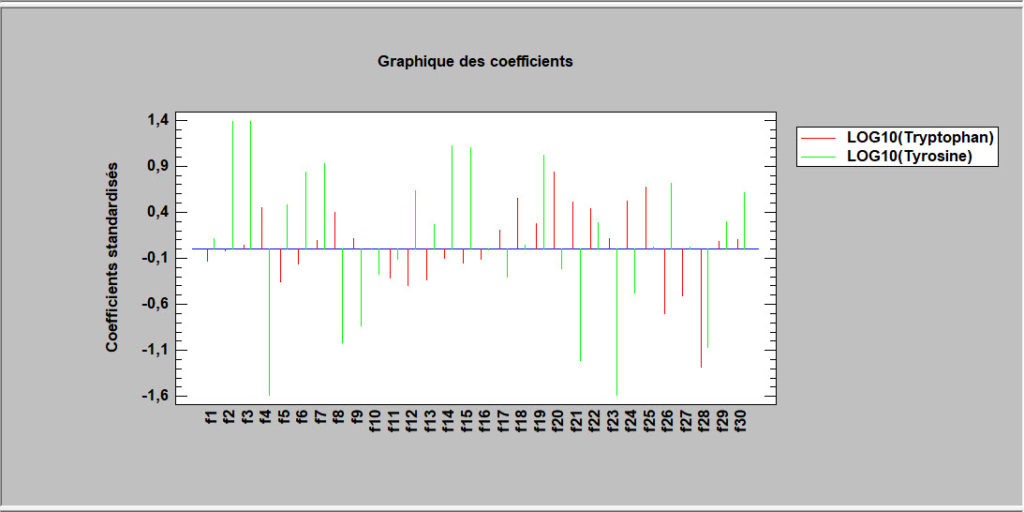
Corrélations canoniques

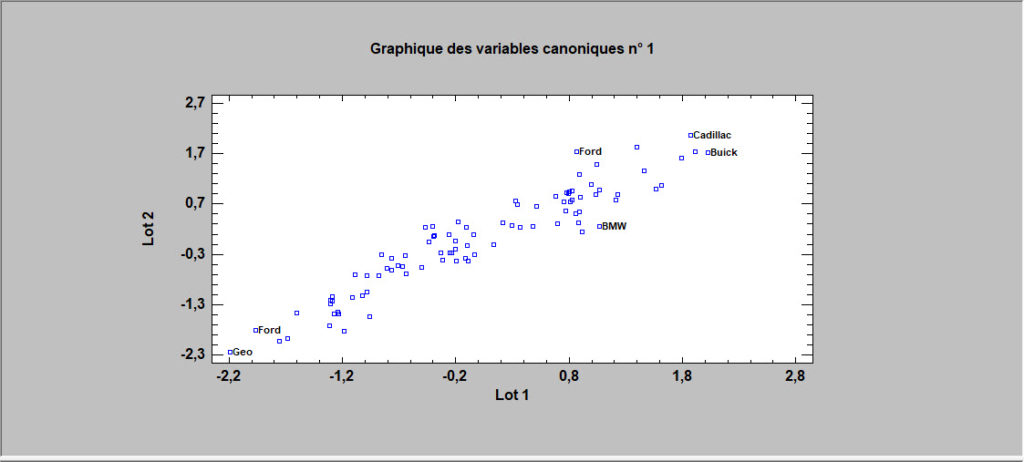
Cette procédure est conçue pour aider à identifier les associations entre deux lots de variables. Elle le fait en trouvant les combinaisons linéaires des variables des deux lots qui ont de fortes corrélations. La paire de combinaisons linéaires ayant la plus forte corrélation forme le premier ensemble de variables canoniques. Le deuxième ensemble de variables canoniques est la paire de combinaisons linéaires qui a la deuxième plus forte corrélation et qui n’est pas corrélée avec le premier ensemble de variables canoniques. Souvent, un petit ensemble de variables canoniques peut être utilisé pour quantifier les relations entre les deux lots de variables.

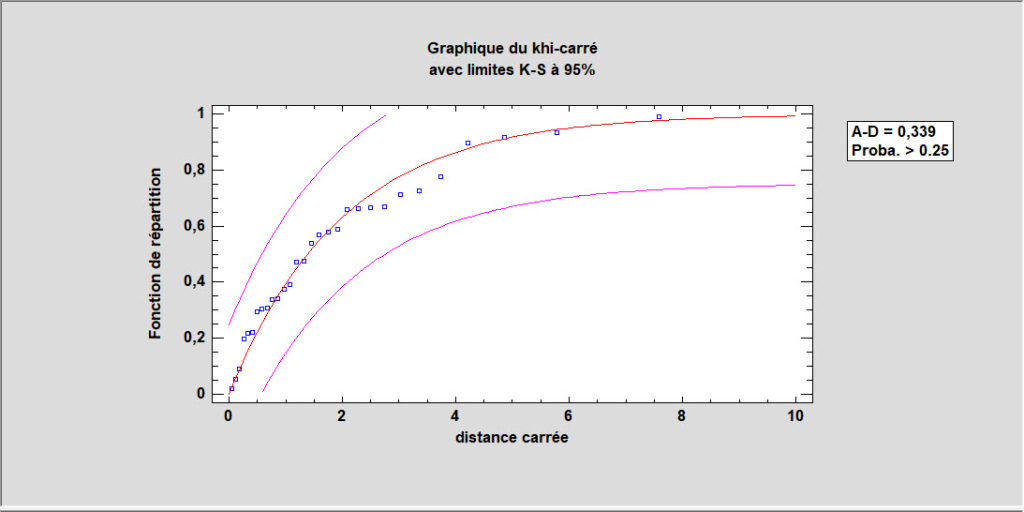
Test de normalité multivariée

Cette procédure teste si un ensemble de variables aléatoires peut raisonnablement provenir d’une loi normale multivariée. Elle inclut le test H Royston et des tests basés sur un graphique du khi-carré de la distance carrée de chaque observation au centroïde de l’échantillon.

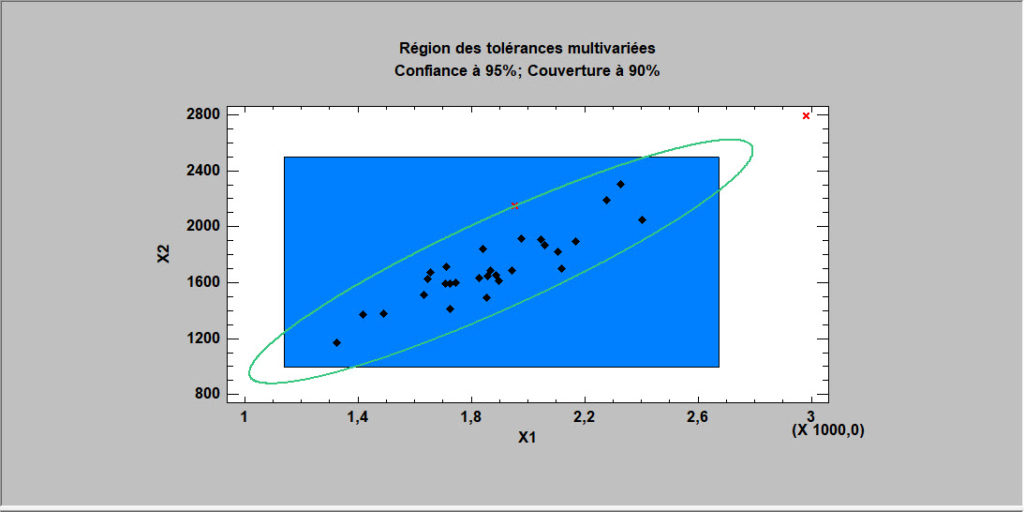
Limites de tolérances multivariées

Cette procédure affiche des limites de tolérances pour des données constituées de plus d’une variable. Elle affiche une région des tolérances qui contient un pourcentage donné p de la population avec un niveau de confiance de 100(1-alpha)%. Elle inclut également des limites simultanées des tolérances pour chaque variable en utilisant l’approche de Bonferroni. Les données sont supposées être un échantillon aléatoire provenant d’une loi normale multivariée. Les limites de tolérances multivariées sont souvent comparées aux limites de spécifications pour plusieurs variables pour déterminer si la plus grande partie de la population est à l’intérieur des spécifications.

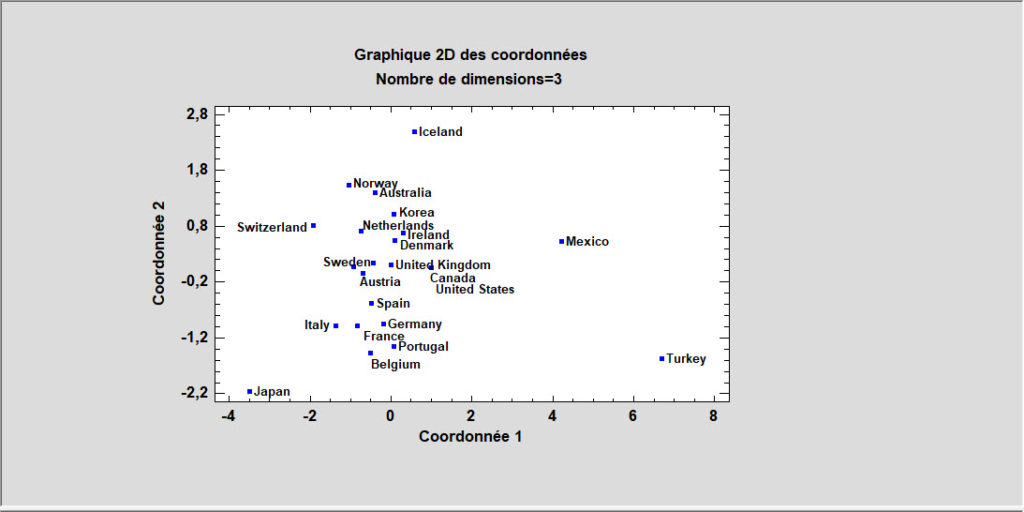
Positionnement multidimensionnel

Cette procédure est conçue pour afficher des données multivariées dans un espace ayant peu de dimensions. A partir d’une matrice de distances n x n entre chaque paire des n observations multivariées, la procédure recherche une représentation de ces observations ayant peu de dimensions et qui préserve les distances entre ces observations le mieux possible. La principale sortie est une carte des points dans un espace de faible dimension (habituellement 2 ou 3 dimensions).