Analyse à une variable

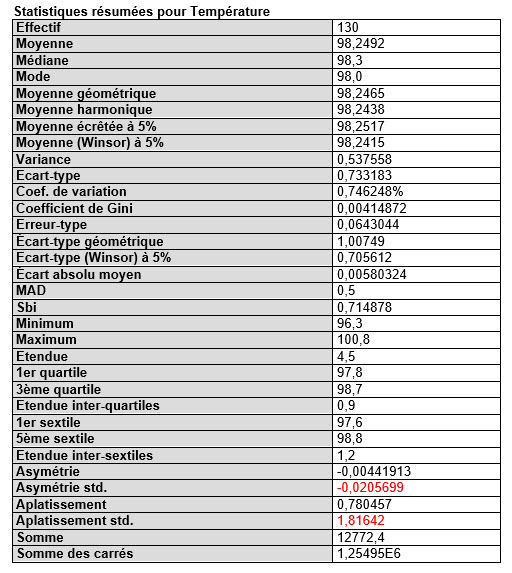
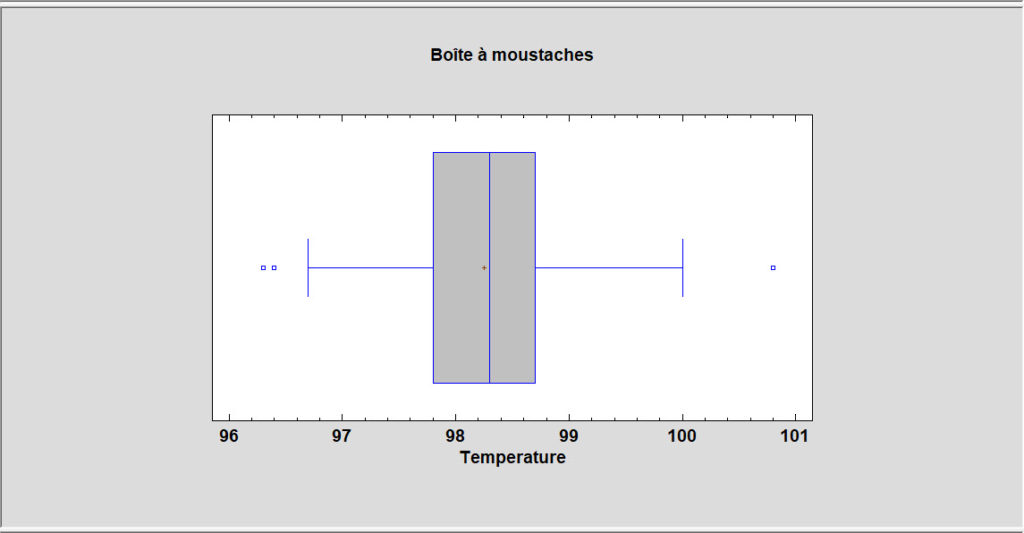
Cette procédure est l’une des principales procédures d’analyse d’une unique colonne de données numériques. Elle calcule des statistiques descriptives et des intervalles de confiance, effectue des tests d’hypothèses et crée une variété de graphiques : nuage de points, histogramme, boîte à moustaches, graphique des quantiles, graphique de normalité, graphique de la densité et graphique de symétrie. Les tableaux incluent les quantiles et un diagramme tiges et feuilles.

Identification des points extrêmes

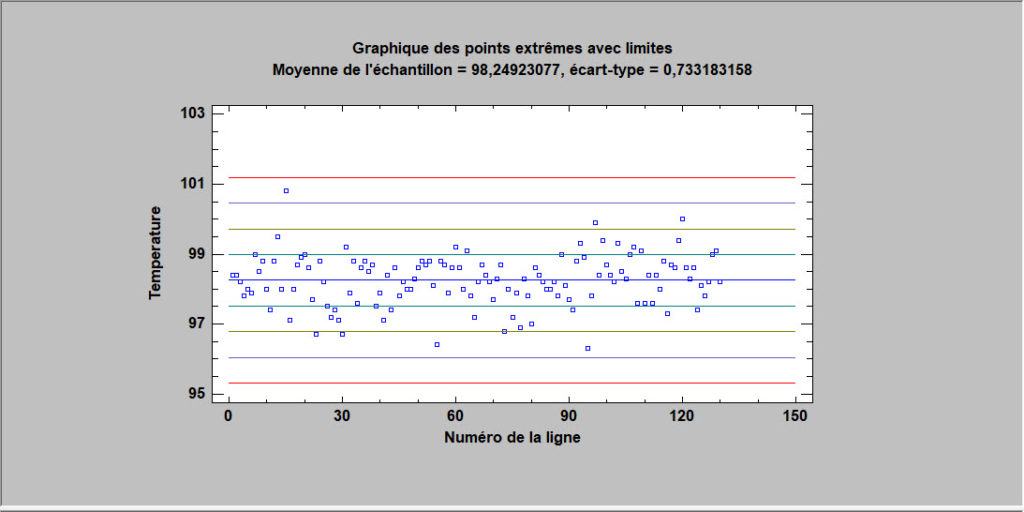
Cette procédure est conçue pour aider à déterminer si un échantillon d’observations numériques contient ou non des valeurs aberrantes. Les valeurs aberrantes sont des observations qui ne proviennent pas de la même distribution que le reste de l’échantillon. Les méthodes graphiques et les tests statistiques formels dus à Grubbs et Dixon sont inclus. La procédure enregistrera également une colonne d’indicateurs identifiant les valeurs aberrantes sous une forme qui peut être utilisée pour exclure ces observations lors de l’exécution d’autres procédures.

Comparaison de deux échantillons

Cette procédure est conçue pour comparer deux échantillons indépendants de données quantitatives. Des tests sont mis en œuvre pour déterminer s’il existe ou non des différences significatives entre les moyennes, les variances, les médianes des populations à partir desquelles les échantillons ont été prélevés. De plus, les données peuvent être affichées graphiquement de diverses manières, y compris un histogramme double, un graphique en boîtes à moustaches multiples et un graphique quantiles-quantiles.

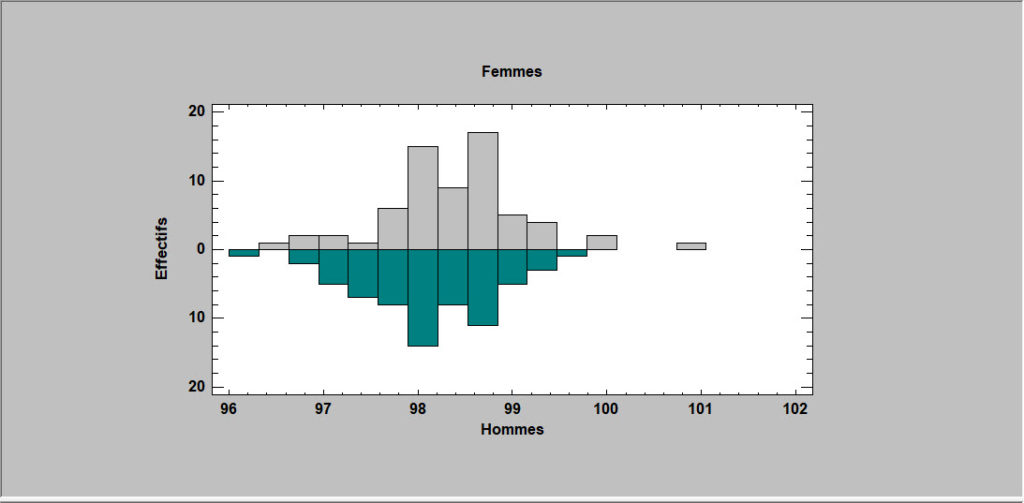
Comparaison d’échantillons appariés

Cette procédure est conçue pour comparer les données dans deux colonnes numériques dans lesquelles les valeurs de chaque ligne sont appariées, c’est-à-dire correspondent au même sujet ou à la même unité expérimentale. La principale raison d’une telle comparaison est généralement de déterminer si oui ou non le facteur qui différencie les colonnes a un effet significatif sur les données.

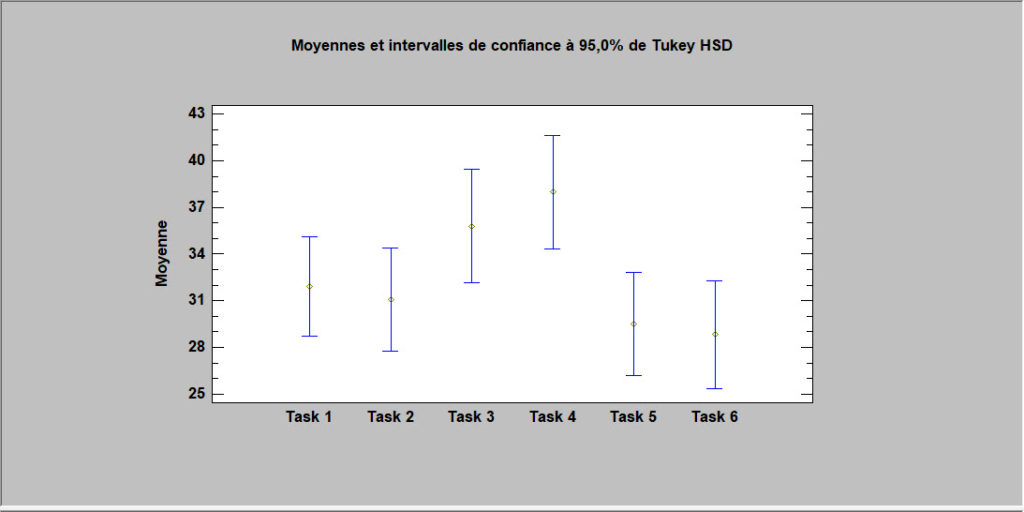
Comparaison de plusieurs échantillons

Cette procédure est conçue pour comparer deux ou plusieurs échantillons indépendants de données quantitatives. Des tests sont mis en œuvre pour déterminer s’il existe ou non des différences significatives entre les moyennes, les variances et les médianes des populations à partir desquelles les échantillons ont été prélevés. De plus, les données peuvent être affichées graphiquement de diverses manières : nuage de points, graphique des moyennes, graphique ANOM et un graphique des médianes.

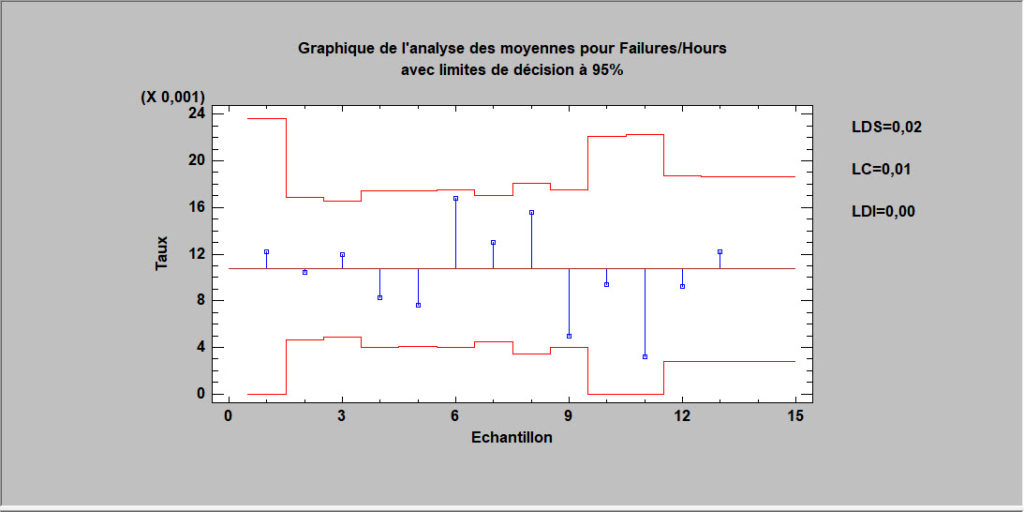
Comparaison de taux et de proportions

Des procédures sont également disponibles pour comparer les taux observés d’un événement parmi les échantillons (sur la base d’une distribution de Poisson) ou pour comparer les proportions observées (sur la base d’une distribution binomiale). Les tests fournis comprennent un test de dispersion, un test du khi-carré et un test du rapport de vraisemblance. Les procédures effectuent également une analyse des moyennes (ANOM) pour déterminer quels échantillons diffèrent significativement de la moyenne globale.

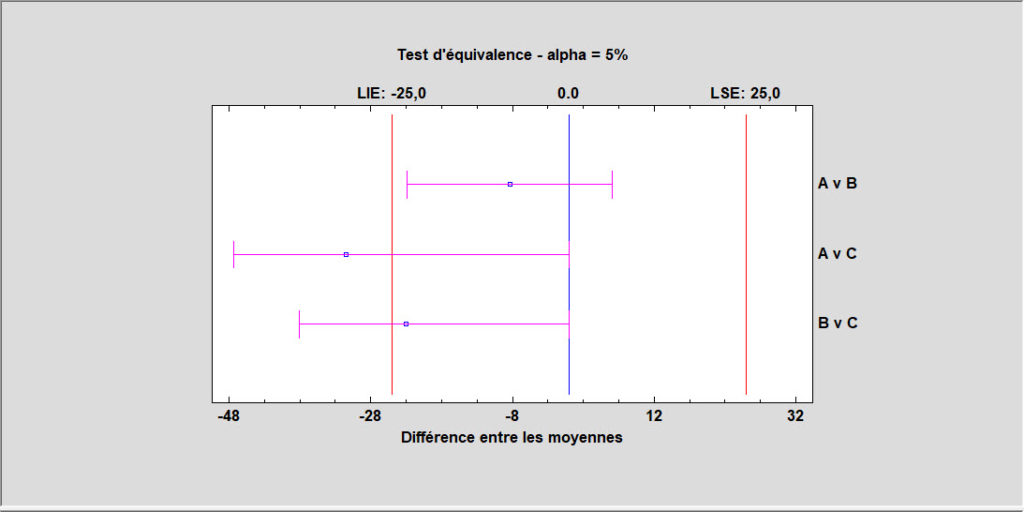
Tests d’équivalence et de non infériorité pour des moyennes

Quatre procédures sont disponibles pour démontrer l’équivalence (bilatérale) ou la non-infériorité (unilatérale) des moyennes. Elles sont utilisées pour comparer deux moyennes indépendantes, comparer deux moyennes appariées, comparer une seule moyenne à une valeur cible et analyser les résultats d’une étude croisée 2×2. Contrairement aux tests d’hypothèse standard qui sont conçus pour prouver la supériorité d’une méthode sur une autre, les tests d’équivalence sont conçus pour prouver que deux méthodes ont essentiellement la même moyenne.

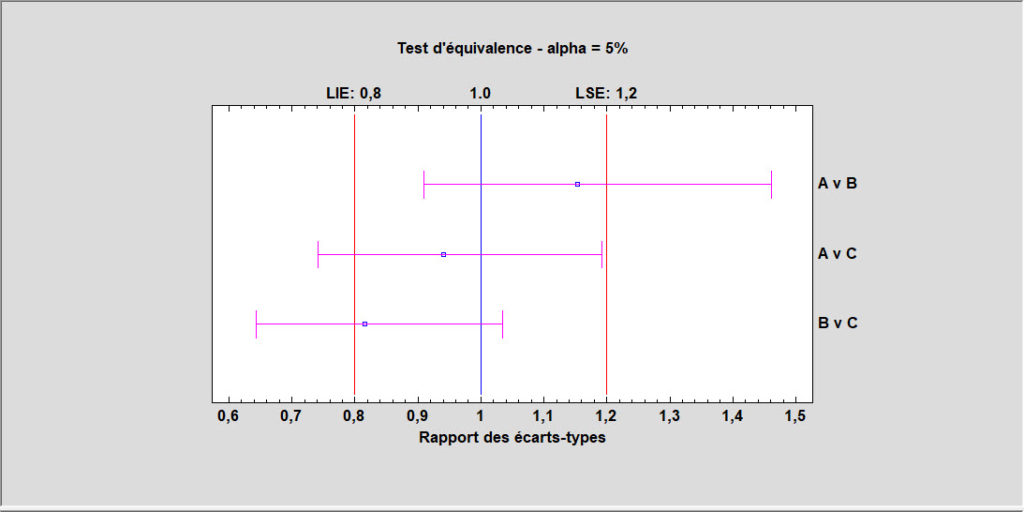
Tests d’équivalence et de non infériorité pour des variances

Deux procédures sont disponibles pour démontrer l’équivalence (bilatérale) ou la non-infériorité (unilatérale) des variances. Elles permettent de comparer deux variances indépendantes et de comparer une seule variance à une valeur cible. Contrairement aux tests d’hypothèse standard qui sont conçus pour prouver la supériorité d’une méthode sur une autre, les tests d’équivalence sont conçus pour prouver que deux méthodes ont essentiellement la même variance.

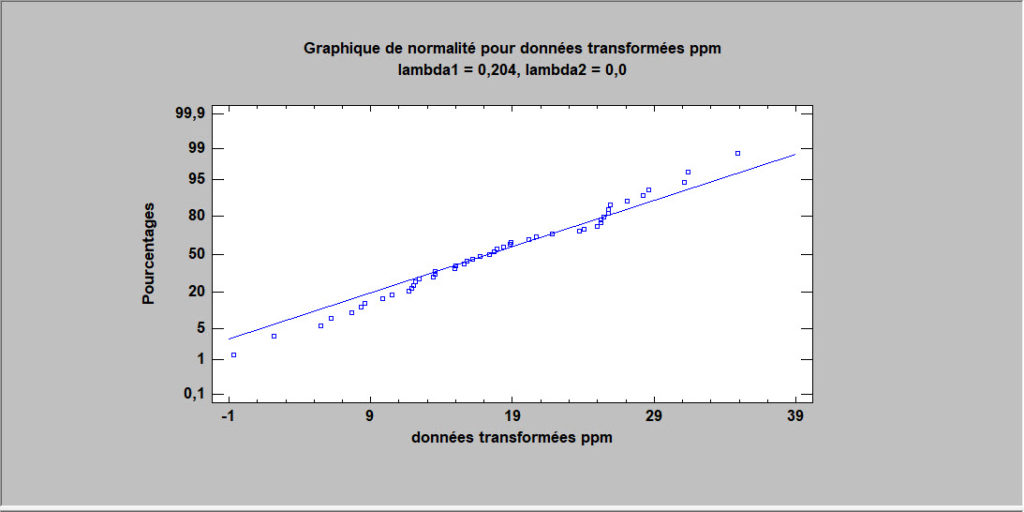
Transformations par puissances

Cette procédure est conçue pour déterminer une transformation de normalisation pour une colonne d’observations numériques qui ne proviennent pas d’une distribution normale. Dans de tels cas, il est souvent possible de trouver une transformation de puissance qui rendra les données approximativement normales. Compte tenu d’une telle transformation, des procédures statistiques qui supposent la normalité peuvent alors être appliquées aux données transformées.