La simulation Monte-Carlo est utilisée pour estimer la distribution des variables lorsqu’il est impossible ou peu pratique de déterminer théoriquement cette distribution. Elle est utilisée dans de nombreux domaines, notamment l’ingénierie, la finance et le DFSS (Design for Six Sigma). Une simulation Monte-Carlo classique est basée sur une ou plusieurs variables d’entrée X, dont certaines suivent généralement une loi de probabilités, une ou plusieurs variables de sortie Y, dont les distributions sont recherchées, un modèle mathématique couplant les X et les Y. Statgraphics contient également un large éventail de générateurs de nombres aléatoires à utiliser dans les modèles de simulation.
Simulation Monte-Carlo
Modèles généraux de simulation
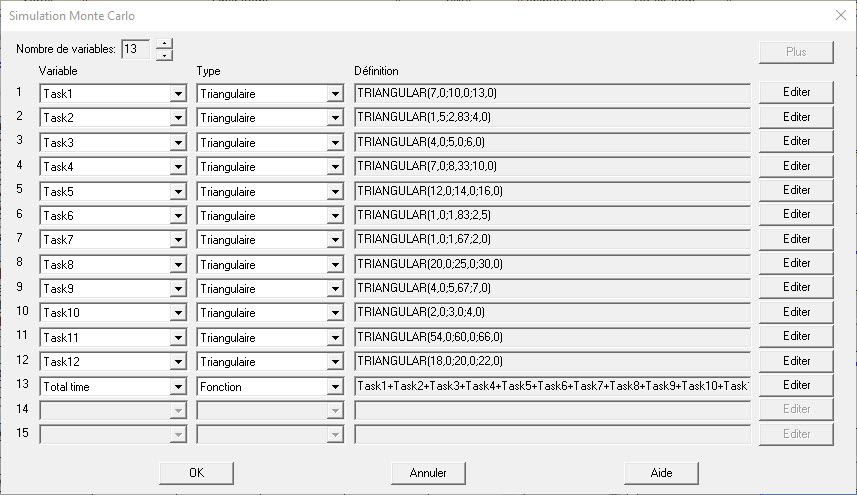
Cette procédure permet de trouver la distribution d’une ou plusieurs variables de sortie définies par des modèles mathématiques les couplant à une ou plusieurs variables d’entrée. Une distribution de probabilité pour chaque variable d’entrée peut être spécifiée. Les quantiles estimés pour les variables de sortie sont calculés et des histogrammes, boîtes à moustaches et graphiques de sensibilité (tornade) sont affichés.
Modèles de simulation ARIMA
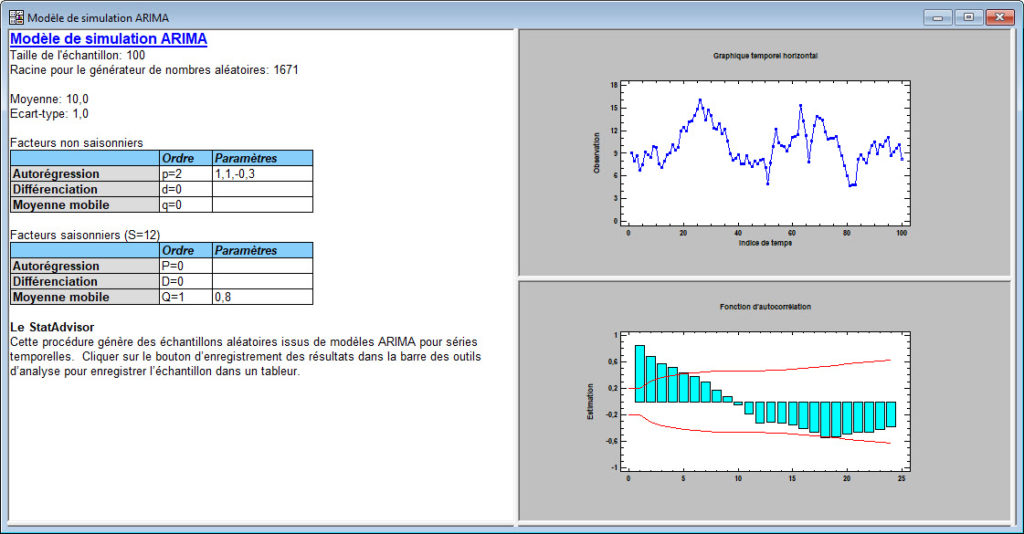
Cette procédure génère des nombres aléatoires à partir de modèles de séries chronologiques ARIMA.
Génération de nombres aléatoires
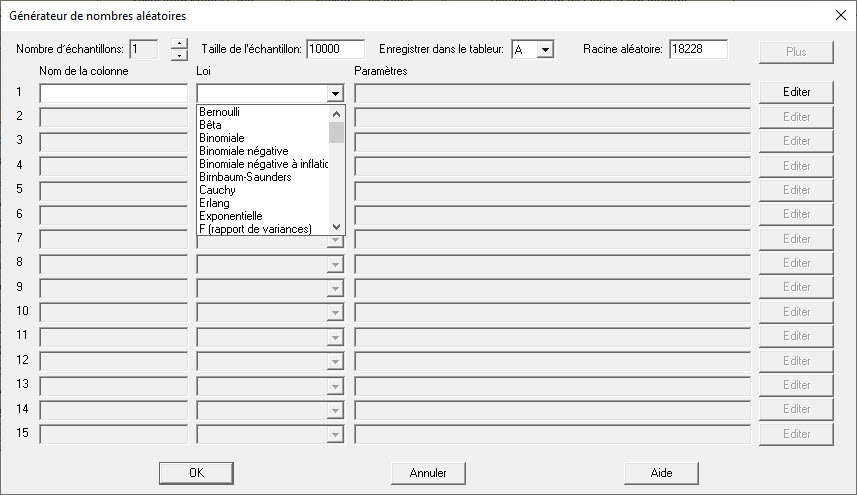
Il est souvent nécessaire de générer des nombres aléatoires à partir de différentes lois de probabilité. Cette procédure simplifie le processus de génération d’échantillons de nombres aléatoires. 49 lois de probabilité sont disponibles.
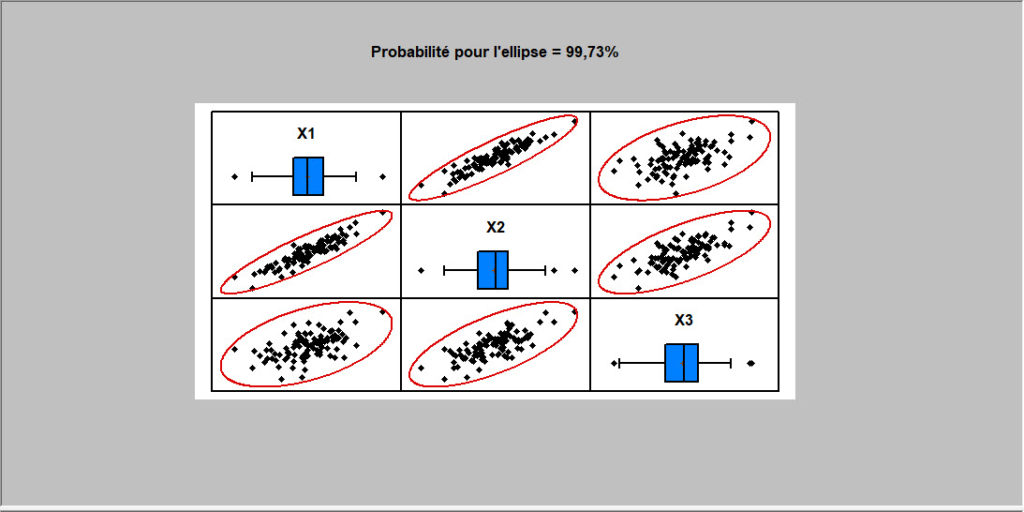
Nombres aléatoires pour une loi normale multivariée
Cette procédure génère des nombres aléatoires à partir d’une loi normale multivariée impliquant jusqu’à 12 variables. L’utilisateur saisit les moyennes variables, les écarts-types et la matrice des corrélations. Des échantillons aléatoires sont générés et peuvent être enregistrés dans le classeur de Statgraphics.