Modèle statistique

Par exemple, considérons le cas d’un circuit électronique conçu pour fonctionner à une tension et à une température spécifiées. Un ingénieur souhaite estimer la durée pendant laquelle un circuit est susceptible de fonctionner correctement. Plus précisément, l’ingénieur souhaite connaître le temps moyen avant défaillance (MTTF) ainsi que les différents quantiles de la loi des temps des défaillances. Toutefois, si le circuit a été bien conçu, il ne sera probablement pas pratique de le tester dans des conditions de fonctionnement normales, car il faudrait trop de temps pour observer suffisamment de défaillances pour être significatif. Au lieu de cela, les tests sont souvent exécutés à des températures et des tensions plus élevées, où les temps des défaillances sont plus courts. Les résultats sont ensuite extrapolés aux conditions normales de fonctionnement à l’aide d’un modèle de régression ajusté.

La version 19.6 de Statgraphics Centurion inclut une nouvelle procédure pour estimer les modèles de tests de durée de vie accélérés couramment utilisés. Deux classes générales de modèles peuvent être adaptées :

1. modèles position-échelle : modèles dans lesquels le temps avant défaillance est exprimé en fonction d’un ou plusieurs facteurs accélérateurs plus un terme d’erreur. Dans de tels cas, on suppose généralement que les temps des défaillances suivent une loi normale, logistique ou plus petite valeur extrême.
2. modèles log-position et log-échelle : modèles dans lesquels le logarithme du temps avant défaillance est exprimé en fonction d’un ou plusieurs facteurs accélérateurs plus un terme d’erreur. Dans de tels cas, les temps des défaillances sont généralement supposés suivre une loi log-normale, log-logistique, exponentielle ou Weibull.

Il existe également plusieurs modèles d’accélération couramment utilisés, comme indiqué dans la boîte de dialogue ci-dessous :

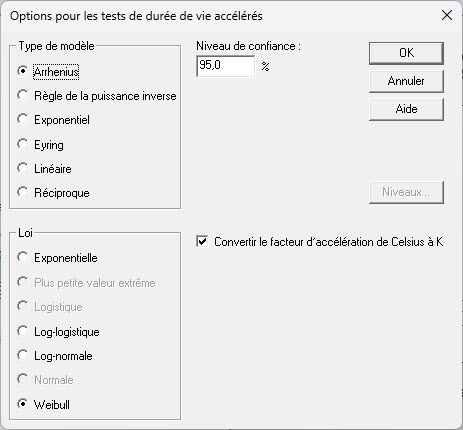
Si la variable accélératrice est la température, on utilise souvent le modèle d’Arrhenius, qui prend la forme suivante :

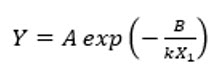
où Y est le temps de défaillance, X₁ est la température en degrés Kelvin (°C + 273.15), k = 0,00008617 (constante de Boltzmann) et A et B sont deux paramètres inconnus. En prenant le logarithme des deux côtés, cela montre que le logarithme du temps de défaillance et linéairement relié à l’inverse de la température :

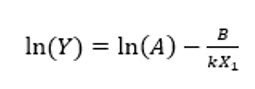
Des facteurs accélérateurs supplémentaires tels que la tension peuvent être introduits en ajoutant des termes supplémentaires à l’équation ci-dessus.

Données de l’exemple

À titre d’exemple, considérons les données présentées ci-dessous :

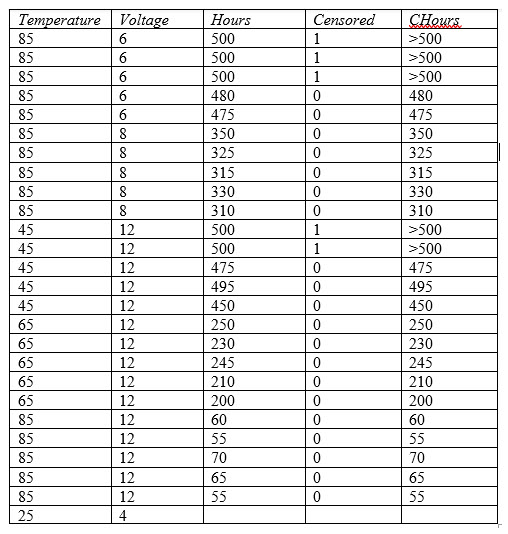
Les données ont été collectées à Température = 45, 65 et 85 degrés centigrades et à Tension = 6, 8 et 12 volts. Les heures représentent soit les temps avant défaillances de chaque élément, soit 500 si l’élément n’a pas été défaillant après 500 heures. Censuré est défini à 0 pour les temps réels des défaillances ou à 1 si un élément n’a pas été défaillant après 500 heures. Une colonne supplémentaire nommée CHours est également affichée, qui est une colonne de données numériques censurées spéciale. Dans cette colonne, les valeurs censurées à droite sont représentées par la notation >500.

Le but de l’étude est d’estimer la distribution des temps des défaillances dans des conditions de fonctionnement normales où Température = 25 et Tension = 4. Notez que ces valeurs ont été ajoutées au bas du tableur, avec la cellule Heures laissée vide. La procédure Statgraphics Tests de durées de vie accélérés reconnaîtra automatiquement cette combinaison de facteurs comme celle pour laquelle des prévisions sont souhaitées.

Boîte de dialogue d’entrée des données

La boîte de dialogue d’entrée des données pour cette procédure a la forme suivante :

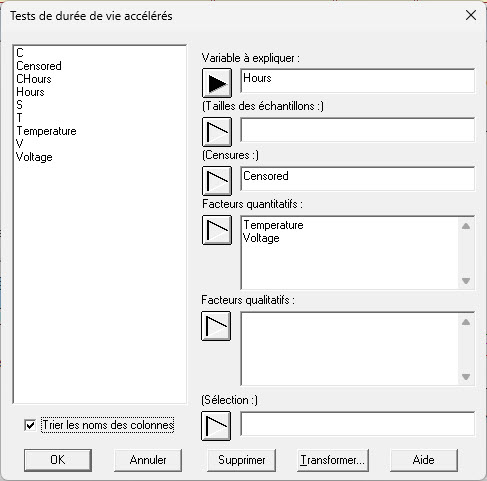
La variable à expliquer est un échantillon des temps des défaillances. Elle peut être :

1. une colonne numérique normale. Dans de tels cas, le champ Censures est utilisé pour indiquer si la ligne représente ou non un temps de défaillance non censuré (indiqué par la saisie d’un 0), un temps censuré à droite (indiqué par la saisie d’un 1) ou un temps censuré à gauche (indiqué en saisissant un -1).
2. une colonne numérique censurée spéciale. Dans de tels cas, le champ Variable à expliquer est utilisé pour indiquer si la ligne représente ou non un temps de défaillance non censuré (indiqué par la saisie d’un nombre tel que 475), un temps censuré à droite (indiqué par la saisie d’une expression telle que >500), un temps censuré à gauche (indiqué par la saisie d’une expression telle que <50) ou une observation censurée par intervalle (indiquée par la saisie d’une expression telle que [300,350]). Le champ Censures n’est pas utilisé.

Si plusieurs échantillons ont les mêmes caractéristiques, comme les 3 premières lignes du fichier de données présenté ci-dessus, le champ Tailles des échantillons peut être utilisé pour spécifier le nombre d’échantillons représentés par chaque ligne du fichier.

Les champs Facteurs quantitatifs et Facteurs qualitatifs indiquent les variables explicatives. Il doit y avoir au moins 1 facteur quantitatif, le premier facteur saisi étant considéré comme le facteur principal d’accélération (température dans ce cas). Comme nous le verrons ci-dessous, différents modèles d’accélération peuvent être choisis pour le facteur principal. D’autres facteurs tels que la tension seront saisis sous forme de termes linéaires dans le modèle de régression. Si un modèle réciproque est souhaité pour d’autres facteurs, saisissez-les dans la boîte de dialogue d’entrée des données en entrant des expressions telles que 1/Tension.

Options d’analyse

Après avoir spécifié les données d’entrée, une boîte de dialogue Options d’analyse s’affiche.

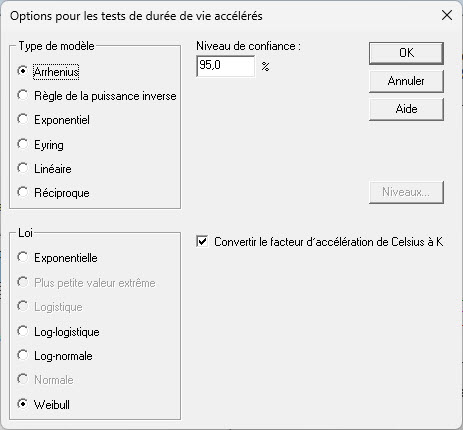
Cette boîte de dialogue permet de sélectionner le type de modèle d’accélération pour le facteur principal. Il permet également de sélectionner la loi des temps des défaillances. En fonction de la loi choisie, un certain nombre de paramètres doivent être estimés. Par exemple, la loi de Weibull a 2 paramètres : un paramètre de forme et un paramètre d’échelle. Le paramètre de forme est supposé avoir une valeur constante qui ne dépend pas des variables explicatives. Par contre, la valeur du paramètre d’échelle se modifie en fonction des variables explicatives. Une loi typique de Weibull est présentée ci-dessous :

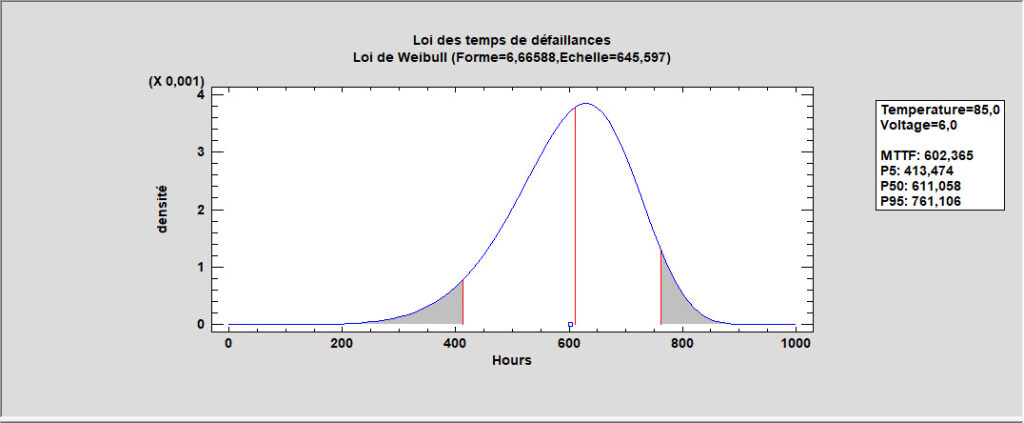
Résumé de l’analyse

L’ajustement du modèle demandé aux données génère un résumé d’analyse qui montre le modèle ajusté. Il est affiché ci-dessous :

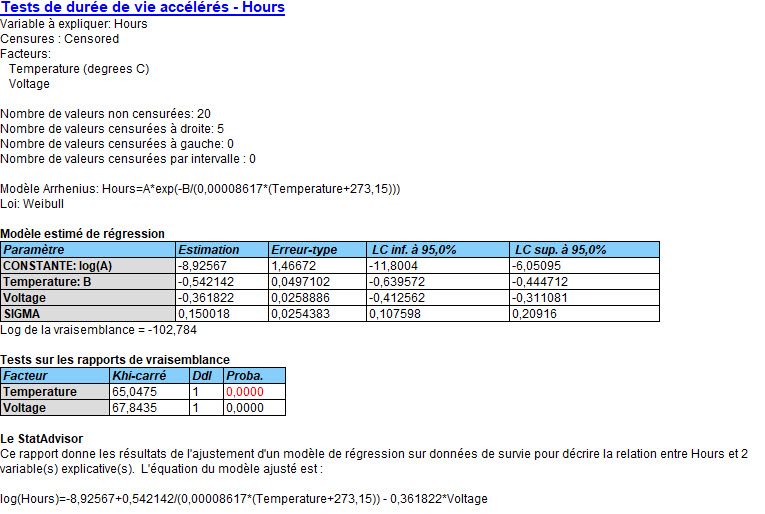
Le modèle estimé pour log(Hours) utilise l’inverse de la température après l’avoir convertie en degrés Kelvin et une fonction linéaire de la tension. Une augmentation de l’une ou l’autre variable explicative entraîne une prévision inférieure pour log(Hours). Un paramètre supplémentaire sigma a également été estimé et est lié à la dispersion de la loi des temps des défaillances.

Loi des temps des défaillances

La loi des temps des défaillances pour les données de l’exemple est supposée être une loi de Weibull, qui a la forme suivante :

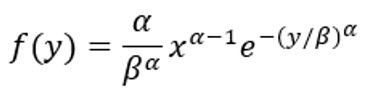
où alpha est le paramètre de forme et bêta est le paramètre d’échelle. Pour toute combinaison des variables explicatives, les paramètres peuvent être déterminés en résolvant les équations suivantes :

On peut voir que le paramètre d’échelle est fonction des variables explicatives, mais pas le paramètre de forme. Le paramètre d’échelle est uniquement lié à sigma.

Des équations similaires peuvent être obtenues pour les autre lois.

Vérification du modèle

Avant d’accepter les résultats d’un test de durée de vie accéléré, il est important d’examiner dans quelle mesure le modèle sélectionné et la loi des temps des défaillances correspondent aux données observées. Deux graphiques sont utiles à cet effet. Le premier affiche un tracé des temps des défaillances observés prévus par le modèle sélectionné. Ce graphique pour les données de l’exemple est présenté ci-dessous :

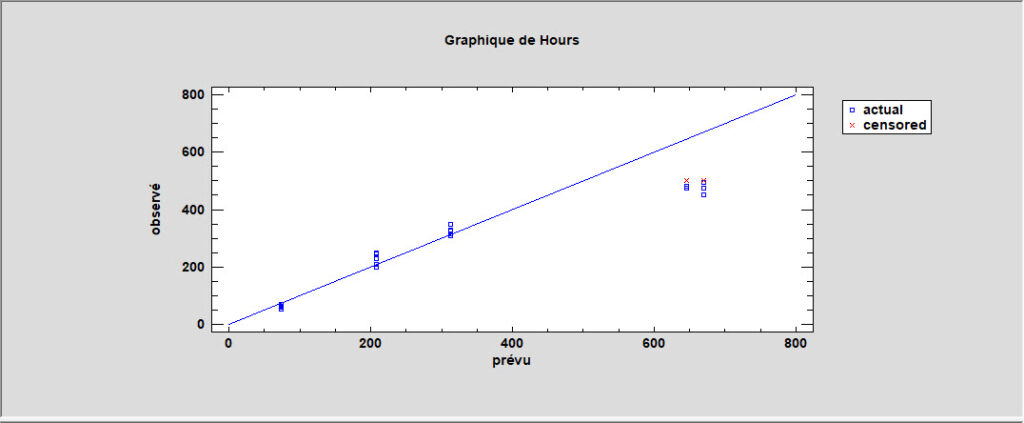
L’écart des prévisions par rapport à la ligne diagonale pour des valeurs d’heures élevées suggère que le modèle surestime le temps avant défaillance pour les valeurs observées les plus élevées. Un graphique de probabilités des résidus basé sur la loi de Weibull montre que les données ne sont pas bien prévues par cette loi, car les points s’écartent considérablement de la ligne diagonale :

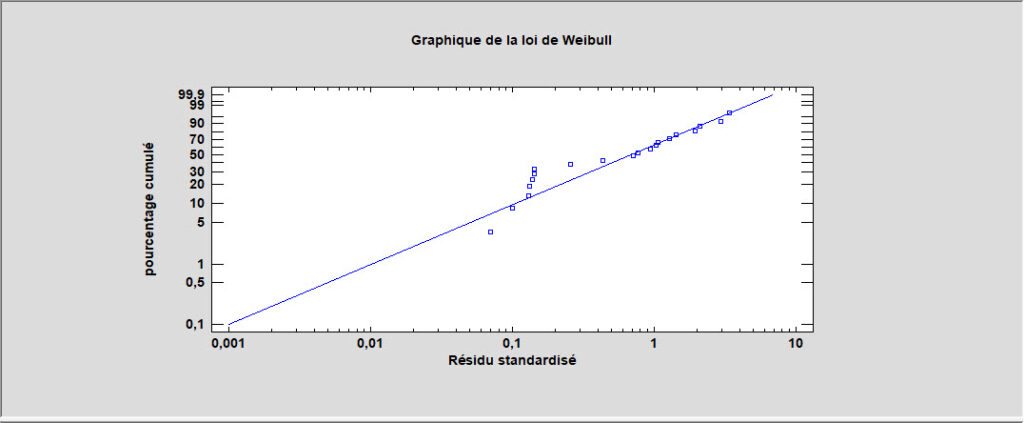
Les essais avec d’autres modèles montrent de bien meilleurs résultats en utilisant un modèle réciproque avec une loi plus petite valeur extrême pour les temps des défaillances :

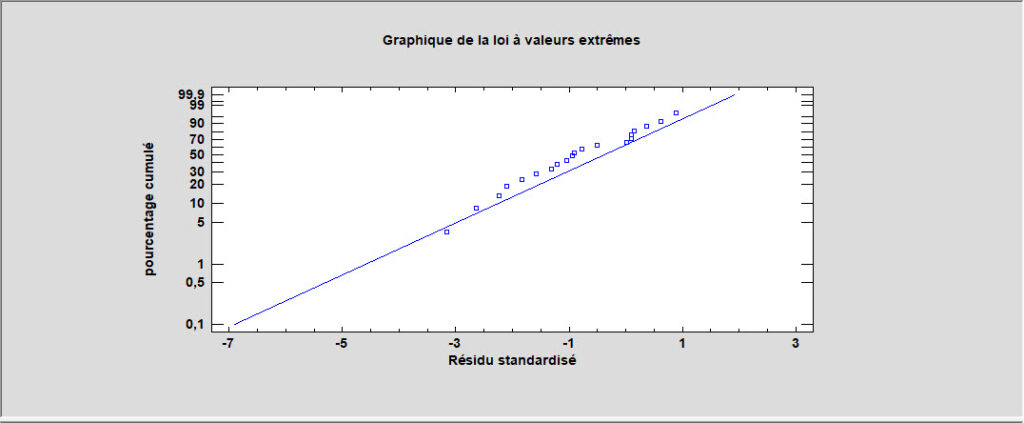
A nouveau, les deux variables explicatives sont très significatives :

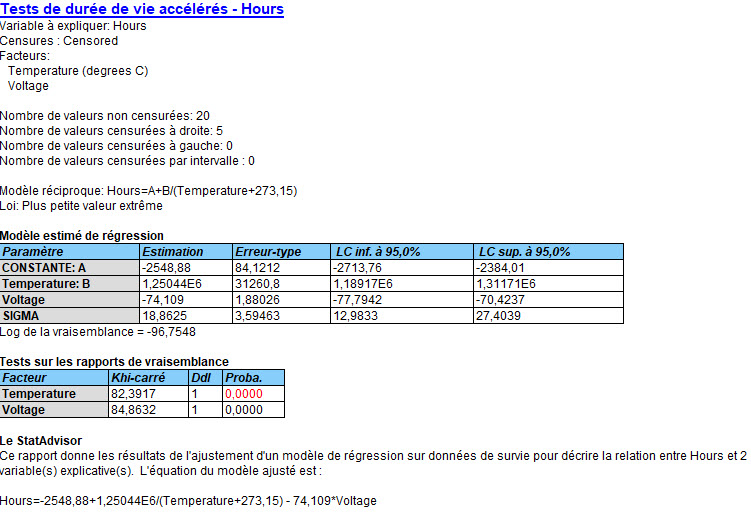
La loi plus petite valeur extrême est définie par 2 paramètres : le mode et un paramètre d’échelle. Le mode est égal à la valeur m générée par l’équation ajustée tandis que le paramètre d’échelle est égal à s.

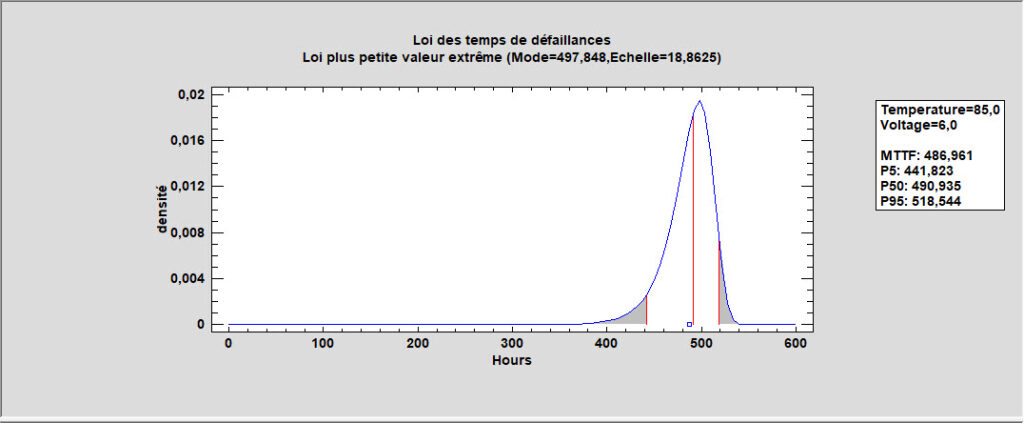
La loi des temps des défaillances présentée ci-dessus est beaucoup plus étroite que la loi précédente de Weibull.

Extrapolation

Pour estimer la loi des temps des défaillances dans des conditions de fonctionnement normales où température = 25 et tension = 4, les équations présentées ci-dessus peuvent être utilisées pour estimer la loi des temps des défaillances comme indiqué ci-dessous :

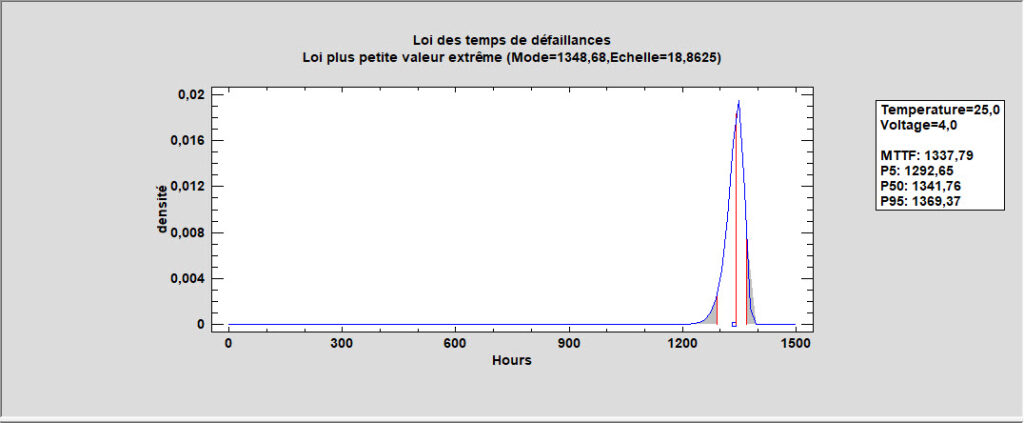
Le temps moyen avant défaillance (MTTF) pour cette combinaison de variables explicatives est estimé à un peu plus de 1300 heures. 90 % de la loi se situe entre environ 1292 et 1369 heures, comme l’indiquent les quantiles estimés.

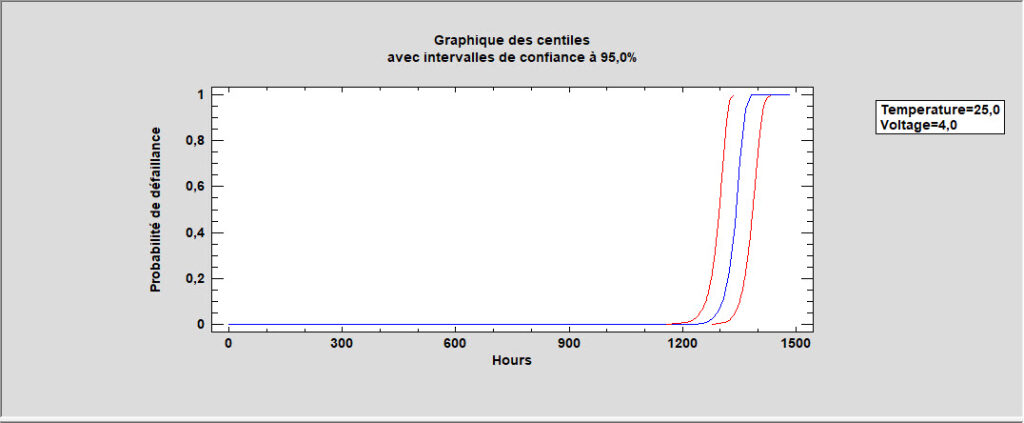
Des limites de confiance peuvent également être calculées pour les quantiles et le temps moyen avant défaillance.

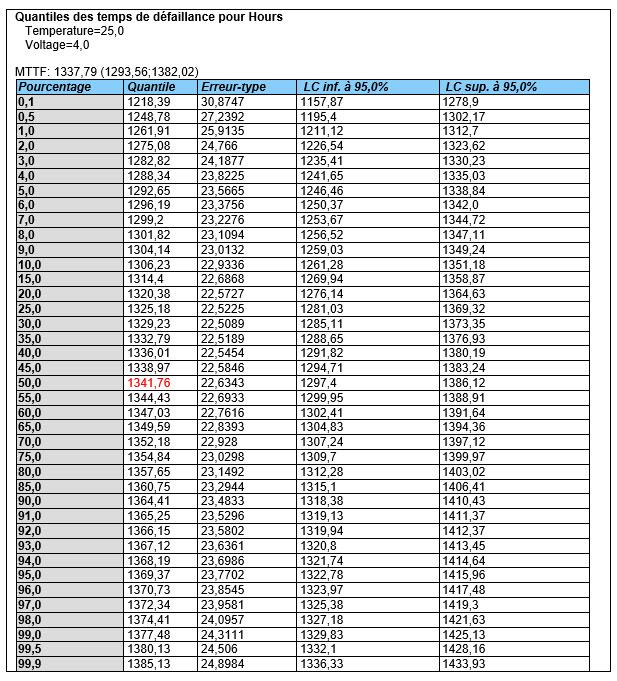
Les quantiles et les limites de confiance peuvent également être affichés graphiquement.

Conclusion

Les tests de durée de vie accélérés peuvent fournir une estimation de la loi des temps des défaillances pour des combinaisons de facteurs de contrainte pour lesquelles l’expérimentation n’est pas faisable. Évidemment, les résultats dépendent du modèle d’accélération sélectionné et de la loi supposée des temps des défaillances. Dans la mesure du possible, ces décisions devraient être prises après avoir examiné les résultats publiés dans des études similaires et vérifiées en examinant les données actuelles.